Hypothesis Testing > Uniformly Most Powerful (UMP) Test
What is a Uniformly Most Powerful Test?
A Uniformly Most Powerful (UMP) test has the most statistical power from the set of all possible alternate hypotheses of the same size α. The UMP doesn’t always exist, especially when the test has nuisance variables (variables that are irrelevant to your study but that have to be be accounted for). However, if the UMP does exist, you can use the Neyman-Pearson lemma (NPL) to find it.
A UMP test is usually defined in terms of a uniformly most powerful rejection region (UMPCR) (also called a “critical region”); A region C of size α is the UMPCR for testing a simple null hypothesis against a set of alternate hypotheses if it is the “best” critical region. The “best” critical region is one that minimizes the probability of making a Type I or a Type II error. In other words, the UMPCR is the region that gives the smallest chance of making a Type I or II error. It is also the region that gives a UMP test the largest (or equally largest) power function.
UMP and the Neyman-Pearson Lemma
The Neyman-Pearson lemma can tell you the best hypothesis test if you have a simple null hypothesis and a simple alternative hypothesis. If you have multiple hypotheses (also called a composite hypothesis), the NPL can be extended to all individual alternate hypotheses. Composite hypotheses have multiple options for solutions. For example, H0:σ2 > 8 is a composite hypothesis because it doesn’t specify a value for σ2; The solution could be anything over 8. This contrasts to H0: μ = 0, which specifies the single value of zero.
The basic idea is that you test each simple hypothesis in turn to see if it is the UMP out of all possibilities.
Definitions using UMP and Likelihood-Ratio
Casella and Berger (2002) define a UMP test as follows:
“Let C be a class of tests for testing H0: θ ∈ Θ0 versus H1: θ ∈ Θc1. A test in class C, with power function β(θ), is a uniformly most powerful (UMP) class C test if β(θ) ≥ β′(θ) for every θ ∈ Θ0c and every β′(θ) that is a power function of a test in class C.
In more simple terms, this is really just telling you that the UMP test is the one with the biggest power function (out of all tests of the same size α). Θ0 is the set of all possible values for θ under the null hypothesis.
The same statement can be rewritten using the likelihood ratio test. Let’s say you had two simple hypotheses H0: θ = θ0 and H1:θ= θ1. In order to find the most powerful test at a certain alpha level (with threshold η), you would look for the likelihood-ratio test which rejects the null hypothesis in favor of the alternate hypothesis when
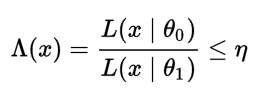
where
![]()
.
If you have an entire set of possibilities (which would be the case with composite hypotheses), each test should be tested individually using the above criteria.
References
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.