U Statistic: Definition, Different Types; Theil’s U

Statistics Definitions >

The term “U statistic” can have several meanings:

1. Unbiased (U) statistics.
2. Mann Whitney U Statistic.
3. U statistic in L-estimators.
4. Theil’s U.

1. Unbiased (U) statistics

Unbiased “U” statistics are a way to construct unbiased estimators to study large sample behavior; the “U” in U-statistics stands for “unbiased”.

Constructing U-statistics involves use of a kernel— a symmetric real valued function h(x,y). An (Unbiased) U statistic is any statistic that can be placed into the following form:



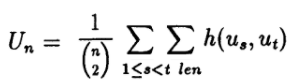
Where:

• (n 2) is the binomial coefficient,
• {u_t} are independent and identically distributed variables.
• Σ = summation notation (“add up”).

Although they look complicated, a U statistic is really just a type of generalized average (Abraham et. al, 2013).

2. Mann Whitney U Statistic

The result of performing a Mann Whitney U Test is a U Statistic. For details on that particular statistic, see: Mann Whitney U Test.

3. L-Estimators

In L-estimation, Kaigh (1983) proposed a type of non-parametric U statistic as a quantile estimator.

4. Theil’s U Statistic

Theil proposed two U statistics, used in finance. The first (U₁) is a measure of forecast accuracy (Theil, 1958, pp 31-42); The second (U₂) is a measure of forecast quality (Theil, 1966, chapter 2).

Wharton University’s J. Scott Armstrong gleaned the following formulae from Theil’s original works; the same formula for U₂ appeared in Brown and Rozeff (1978):

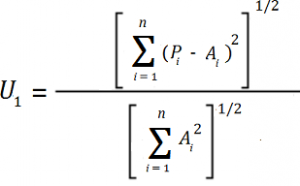
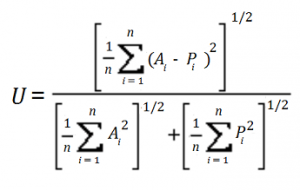
Where:

• A = change in actual earnings,
• P = predicted change in earnings.

If you perform a Google search for Theil’s U, you’ll find an interesting assortment of different formulae, each purporting to be “Theil’s U”. According to Armstrong, the existence of multiple formulas “…has caused some confusion.” For example, the occasional author refers to the Uncertainty Coefficient (unrelated to the U statistic) as Theil’s U, because Theil originally worked on its derivation. The end result is that if you need to use Theil’s U for some reason, the best idea is to refer to Theil’s original formulae, shown above. That said, if you’re reading about Theil’s U in the literature, you may want to make sure that the author is using the correct formula.

References

Abraham, N. et. al (2013). Measures of Complexity and Chaos. Springer Science & Business Media.
Armstrong, J. (No Title). Retrieved December 8, 2017 from: http://armstrong.wharton.upenn.edu/dictionary/definitions/theil%27s%20u.html
Brown, L. & Rozeff, M. (1978). The superiority of analyst forecasts as measures of expectations: Evidence from earnings. In The Journal of Finance, Vol. XXXIII, March. No. 1.
Kaigh, W.D. (1983), “Quantile Interval Estimation,” Communications in Statistics, Part A – Theory and Methods, 12,2427-2443.
Theil, H. (1958), Economic Forecasts and Policy. Amsterdam: North Holland.
Thiel, H. (1966), Applied Economic Forecasting. Chicago: Rand McNally.