Probability Distributions > Trapezoidal Distribution
What is a Trapezoidal Distribution?
Van Dorp & Kotz define the parameters of the distribution as:
- a = minimum value for the random variable,
- b = lower mode (where the constant stage starts),
- c = upper mode (where the constant stage ends),
- d = maximum value for the random variable,
- m = growth rate for the period between a and b,
- n = decay rate for the period between c and d,
- α = boundary ratio, fx(b)/fx(c) which Kotz & Van Dorp define as “the relative likelihood of capabilities at stage [a,b] and the beginning of the decay stage [c, d].”
Note that the mode of this distribution is not unique; it can take on any value between the lower mode c and the upper mode d.
PDF of the Trapezoidal Distribution
The Probability Density Function (PDF) for the trapezoidal distribution (From Dorp & Kotz, 2003) is:
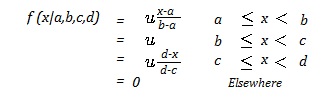
Where:
- μ = 2/(d + c – b – a)-1
- a ≤ b ≤ c ≤ d
CDF
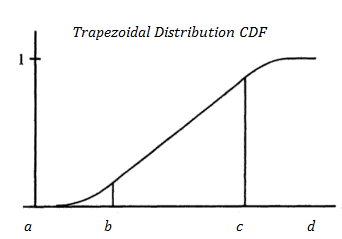
The trapezoidal cumulative distribution function is 0 for x < a and 1 for x ≥ d. Otherwise, it is linear between b and c, and quadratic for a → b and c → d:
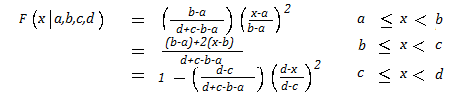
Similar Distributions
- The uniform distribution is a special case of the trapezoidal distribution; It does not have a growth or decay stage so a (the minimum) = c (the lower mode) and d (the maximum) = b (the upper mode).
- The triangular distribution is also a special case of the trapezoidal; It is missing the constant stage so b (the lower mode) = c (the upper mode).
References:
Kotz, S. & Dorp. R. (2004). Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications. World Scientific.
Van Dorp, J et. al,. (2004). An Elicitation Procedure for the Generalized Trapezoidal Distribution with a Uniform Central Stage. Decision Analysis, 4(3):156–166, September 2007.
Van Dorp, J. & Kotz, S.(2003) Generalized Trapezoidal Distributions. Metrika, Vol. 58, Issue 1, July.