Hypothesis Testing > Testing a Single Mean
When you test a single mean, you’re comparing the mean value to some other hypothesized value. Which test you run depends on if you know the population standard deviation(σ) or not.
Known population standard deviation
If you know the value for σ, then the population mean has a normal distribution: use a one sample z-test. The z-test uses a formula to find a z-score, which you compare against a critical value found in a z-table. The formula is:
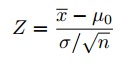
Watch the video for an example of a z-test for a single mean:
Unknown population standard deviation
If you don’t know the population standard deviation, use the t-test. The t-score formula is almost identical to the z-score formula, except that σ (the population standard deviation) has been replaced by s (the sample standard deviation). The formula is:
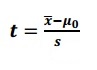
.
The test is run the same way: use the formula to calculate your t-score and then compare it to a value found in a table (this time you’ll use the t-table).
See: One Sample T-Test example.
Non Parametric Tests for Testing a Single Mean
Non parametric (“distribution free”) tests don’t assume your data comes from a certain distribution, like the normal distribution. So if you have data that isn’t normally distributed, you should use one of these alternatives:
- One sample Wilcoxon test (assumes your data comes from a symmetric distribution).
- One sample sign test (has no assumption about the shape of the distribution).
Both tests use medians instead of means. You don’t want to compare means for non-normally distributed data because the mean is very affected by outliers and skewness. As you don’t know the shape of the potential distribution, running a test for a mean would give you a very high probability of your results being wrong. The median on the other hand, is resistant to outliers and changes in skew.
References
Hahs-Vaughn, D. (2020). An Introduction to Statistical Concepts 4th Edition. Routledge.