Contents:
See also: Einstein Summation.
What is Summation Notation?
Watch the video for a few examples, or read on below:
In calculus, summation notation or sigma (Σ) represents adding many values together.
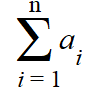
The “ai” in the above sigma notation is saying that you sum all of the values of “a”. In other words, you’re adding up a series of values: a1, a2, a3, …, ax.
- i is the index of summation. It doesn’t have to be “i”: it could be any variable (j, k, x etc.).
- ai is the ith term in the sum.
- n and 1 are the upper and lower bounds of summation. I’m using “1” here as an example: the lower bound could be an integer less than or equal to n.
The following image shows sigma notation for adding up a series of digits from 1 to 6. The lower bound (1) and upper bound (6) are below and above the sigma, respectively. Basically, you start adding at 1 and stop when you get to 6:
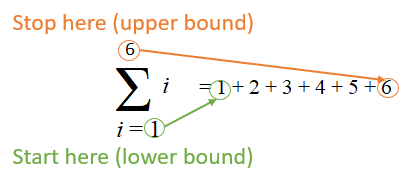
In the following example, “k” is the index of summation because there’s a “k” in the formula.
![]()
It’s telling you to start at k = 1 (lower bound) and keep on summing. It might seem that you keep on adding infinitely, but you’ll usually stop when your function either converges (settles on a certain number) or clearly diverges (shows no hope of convergence).
Using Summation Notation: Calculus Example (Rectangles)
Sigma notation can be used in calculus to evaluate sums of rectangular areas. You can think of the bounds of summation here as where your rectangles start, and where they end.
Example problem: Evaluate the sum of the rectangular areas in the figure below. Use sigma notation:
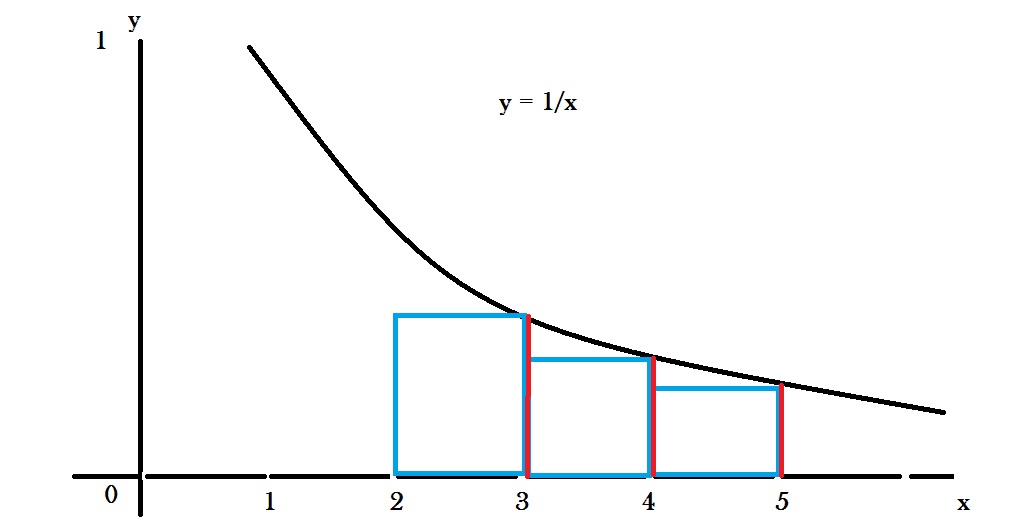
Step 1: Multiply the lengths of the base by the height of each rectangle.
- 1 * 1⁄3 = 1⁄3
- 1 * 1⁄4 = 1⁄4
- 1 * 1⁄5 = 1⁄5
Step 2: Add up the numbers you calculated in Step 1:
1⁄3 + 1⁄4 + 1⁄5 = 47⁄60.
Step 3: Write the summand 1⁄k to the right of the sigma. The variables i, j, and k are usually used instead of x:
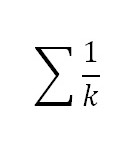
Step 4: Write the place where the summation ends at the top of Σ. This is a right-hand Riemann sum and so the measurement ends at the right of the last rectangle, at x = 5.
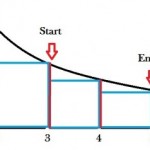
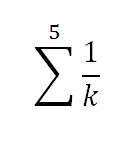
Step 5: Write the place where the summation starts at the bottom of Σ, after the index of summation (in this case, the index of summation is k).
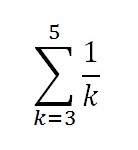
That’s it!
What is a Sigma Function?
The “sigma function” may refer to:
As a Sum of Positive Divisors
In number theory, the Sigma Function (denoted σ(n) or Σ(n)) of a positive integer is the sum of the positive divisors of n. For example, the number 3 has two positive divisors (1, 3) with a sum of 1 + 3 = 4. So:
σ(3) = 4.
A few more examples:
- σ(6) = (1 + 2 + 3) = 6,
- σ(12) = (1 + 2 + 3 + 4 + 6) = 16,
- σ(15) = (1 + 3 + 5) = 9.
Interestingly, the sigma function for any prime number is just that number plus one. That’s because primes are only divisible by itself and one.
The Weierstrass Sigma Function
The Weierstrass sigma function, usually denoted σ(z), is used in complex analysis and elliptic function theory (an elliptic function is a doubly periodic function). It was named after German mathematician Karl Weierstrass (October 1815 – 19 February 1897) and appeared in several of his works.
The Weierstrass elliptic functions, which includes sigma, are in a relatively simple form and are also called p-functions, with a stylized letter P: ℘.
The Weiestrass Sigma function is defined as:
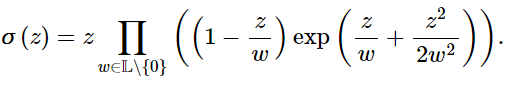
Properties of the Weierstrass Sigma Function
- σ(z) is an odd function of z. Odd functions are symmetrical about the origin.
- σ(z) is an entire function.
References
Caldwell, C. Retrieved November 30, 2019 from: https://primes.utm.edu/glossary/page.php?sort=SigmaFunction
Gaberdiel, J. A Study of Perfect Numbers and Related Topics, With Special Emphasis on the Search for an Odd Perfect Number. Retrieved November 30, 2019 from: https://www.math.arizona.edu/~rta/001/gaberdiel/
Komeda, J. et al. The Sigma Function for Weierstrass Semigroups <3, 7, 8> and <6, 13, 14, 15, 16>. International Journal of Mathematics, Vol. 24, No. 11.
Korn, G. & Korn, T. (2013). Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. Courier Corporation.
Calculus With Precalculus