A semiparametric model is a regression model with both a finite- and an infinite-dimensional component.
A finite-dimensional component is spanned by some list of vectors (a vector is an object that has both magnitude and direction). The two-dimensional and three-dimensional spaces we deal with in everyday geometry are examples of finite-dimensional spaces, but so is a hypothetical 4568-dimensional space. Infinite dimensional spaces are spaces that have an infinite, and possibly ill-defined, number of dimensions and possibilities. They aren’t spanned by any finite list of vectors.
In contrast to parametric models, which are well-defined in the finite-dimensional space, and non-parametric models, where the parameters can all span an infinite space, a semiparametric model has a component that is finite-dimensional (i.e. it’s easy to research and understand), and another that is infinite-dimensional (i.e. beyond the range of ordinary statistical methods).
In research and statistics projects involving semi-parametric models the emphasis is almost always on the parametric component of the model. That’s because this is the part which lends itself well to research.
Why Use Semiparametric Models?
Too often parametric models, while being easy to understand and easy to work with, fail to give a fair representation of what is happening in the real world. Non-parametric models may be better representations but do not lend themselves well to analysis. A semiparametric model allows you to have the best of both worlds: a model that is understandable and can be manipulated while still offering a fair representation of the messiness that is involved in real life.
Examples of Semiparametric Models
One example of a semi-parametric model is the Cox Proportional Hazards Model. This model is very useful in studies of the time remaining before an end or failure; it’s used when doing research on the time remaining before a patient dies, or before a light bulb burns out. It’s defined as:
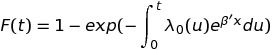
Here x is what we call the covariate vector, and our unknown parameters are Β and λ0 (u). Β is finite-dimensional and is often the subject of research; λ0 (u), on the other hand, is a unknown, non-negative function of time, and the space of λ0 (u) possibilities is infinite. We call it a ‘nuisance parameter‘; a parameter that can’t be entirely omitted in a rigorous treatment of a problem but is not of immediate interest– typically because it is difficult or impossible to study.
Gaussian mixture models are semi-parametric. Parametric implies that the model comes from a known distribution (which is in this case, a set of normal distributions). It’s semi-parametric because more components, possibly from unknown distributions, can be added to the model.