Semi Interquartile Range / Quartile Deviation

Measures of Spread > Semi Interquartile Range / Quartile Deviation

What is the Semi Interquartile Range?

The semi interquartile range (SIR) (also called the quartile deviation) is a measure of spread. It tells you something about how data is dispersed around a central point (usually the mean).

The SIR is half of the interquartile range.

How to Calculate the Semi Interquartile Range / Quartile Deviation

As the SIR is half of the Interquartile Range, all you need to do is find the IQR and then divide your answer by 2.

Another way is to use the quartile deviation formula:

Note: You might see the formula QD = 1/2(Q₃ – Q₁). Algebraically they are the same.

Breaking down the above formula:

Step 1: Find the first quartile, Q₁. If you’re given Q₁ in the question, great. If not, you’ve got several options, including:

Use a calculator, like this one. Plug in your numbers and click the blue button. Q₁ is equal to the 25th percentile listed in the results.
Follow these instructions to find the interquartile range by hand (part of the process is to find quartiles).

Step 2: Find the third quartile, Q₃. If you’re given Q₃ in the question, great. If not, use one of the options listed in Step 1. If you choose to use the calculator, Q₃ is equal to the 75th percentile.

Step 3: Subtract Step 1 from Step 2.

Step 4: Divide by 2.

Example

Question: Find the Quartile Deviation for the following set of data:
{490, 540, 590, 600, 620, 650, 680, 770, 830, 840, 890, 900}

Step 1: Find the first quartile, Q₁.
This is the median of the lower half of the set {490, 540, 590, 600, 620, 650}.
Q₁ = (590 + 600) / 2 = 595.

Step 2: Find the third quartile, Q₃.
This is the median of the upper half of the set {680, 770, 830, 840, 890, 900}.
Q₃ = (830 + 840) / 2 = 835.

Step 3: Subtract Step 1 from Step 2.
835 – 595 = 240.

Step 4: Divide by 2. 240 / 2 = 120

The quartile deviation for this set of data is 12.

Coefficient of Quartile Deviation

The coefficient of quartile deviation (sometimes called the quartile coefficient of dispersion) allows you to compare dispersion for two or more sets of data. The formula is:

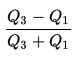
If one set of data has a larger coefficient of quartile deviation than another set, then that data set’s interquartile dispersion is greater.