Statistics Definitions > Scale Invariance
What is Scale Invariance?
A system, function, or statistic has scale invariance if changing the scale by a certain amount does not change the system, function, or statistic’s shape or properties. Fractals are one of the more well known examples of this. For example, if you zoom in on a Koch snowflake, it looks the same.
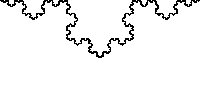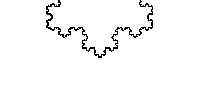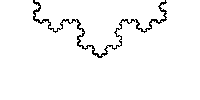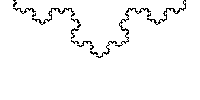
.
Scale Invariant Statistics
Any object, function, or statistic that doesn’t change when scales are multiplied by a common factor is scale invariant. In statistics, it can also mean a statistic that tends not to change (i.e. 99% of the time, it will stay the same).
Some specific statistics are scale invariant. For example, Anderson (1993) noted that Hotelling’s T-Statistic is scale invariant. Each observation, the mean and the standard deviation can all be multiplied by a constant c, and the statistic is unaffected.
More Specific Definitions
“Scale invariance” is one of those terms that’s loosely defined; it’s often used interchangeably with “self-similarity”, although technically they aren’t exactly the same. Self-similarity means that a whole or a small part of an object looks exactly the same, or more specifically, that the function is the same under a discrete subset of dilations. Scale invariance means that the object will look the same even if the scale is changed. The definition of scale invariance is slightly different depending on where you’re using it (Zohuri, 2015):
- Mathematics: scale invariance means the invariance of functions or curves, or probability distributions of random variables.
- Statistical Mechanics: a feature of phase transitions where you try to find a scale invariant theory to describe fluctuating phenomena.
- Physics: generally refers to invariance of an entire theory. In particle physics, a scale-invariant theory is “the strength of particle interactions does not depend on the energy of the particles involved.”
References:
Anderson, T.W. (1993). Introduction to Hotelling (1931) The Generalization of Student’s Ratio. In Breakthroughs in Statistics: Foundations and Basic Theory.
Zohuri, B. (2015). Dimensional Analysis and Self-Similarity Methods for Engineers and Scientists. Springer.