There isn’t a universal definition for the “reciprocal distribution.” Definitions from the literature include:
- Any distribution of a reciprocal of a random variable [1]).
- A reciprocal continuous random variable [2].
- A synonym for the logarithmic distribution [3].
That said, most PDFs for a reciprocal distribution involve a logarithm in one form or another: for pink noise, distributions of mantissas (the part of a logarithm that follows the decimal point), or the under-workings of Benford’s law.
Of all the different versions of the probability distribution function (PDF) for the reciprocal distribution, the pink noise/Bayesian inference one is by far the most common.
1. Pink Noise / Bayesian Inference
The reciprocal distribution is used to describe pink (1/f) noise, or as an uninformed prior distribution for scale parameters in Bayesian inference.
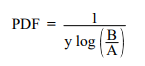
SciPy stats also uses this PDF.
2. Distribution of Mantissas
The mantissa is the part of the logarithm following the decimal point, or the part of the floating point number (closely related to scientific notation) following the decimal point. For example, .12345678 * 102, .12345678 is the mantissa.
In his book, Numerical Methods for Scientists and Engineers, Richard Hamming uses a reciprocal distribution to describe the probability of finding the number x in the base b (The base in logarithmic calculation is the subscript to the right of “log”; the base in log3(x) is “3”). The pdf for this probability is:
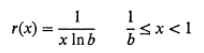
3. Reciprocal Distribution (Benford’s Law)
The reciprocal distribution is a continuous probability distribution defined on the open interval (a, b). The Probability Density Function (PDF) is r(x) ≡ c/x,
Where:
- x = a random variable,
- c = the normalization constant c = 1/ ln b (when x ranges from 1/b to 1).
This PDF is the underpinnings of Benford’s Law [6].
4. Other Uses and Meanings
Outside of probability and statistics, the term “reciprocal distribution” doesn’t involve a probability distribution at all; it refers to You scratch my back and I’ll scratch yours. For example “Reciprocal distribution of raw materials is only fair—”.
References
[1] Marshall, A. & Olkin, L. (2007). Life Distributions: Structure of Nonparametric, Semiparametric, and Parametric Families.
[2] SciPy Stats (2009). scipy.stats.reciprocal. Retrievd December 11, 2017 from: https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.reciprocal.html
[3] Bose, P. & Morin, P. (2003). Algorithms and Computation: 13th International Symposium, ISAAC 2002 Vancouver, BC, Canada, November 21-23, 2002, Proceedings.
[4] McLaughlin, M. (1999). Regress+: A Compendium of Common Probability Distributions. Retrieved 5/18/23 from http://www.ub.edu/stat/docencia/Diplomatura/Compendium.pdf
[5] Hamming, R. (2012). Numerical Methods for Scientists and Engineers. Courier Corporation.
[6] Friar et al., (2016). Ubiquity of Benford’s law and emergence of the reciprocal distribution. Physics Letters A, Volume 380, Issue 22-23, p. 1895-1899.