What is the Rayleigh Distribution?
The Rayleigh distribution is a continuous probability distribution named after the English Lord Rayleigh. It is a special case of the Weibull distribution with a scale parameter of 2. When a Rayleigh is set with a shape parameter (σ) of 1, it is equal to a chi square distribution with 2 degrees of freedom.
The notation X Rayleigh(σ) means that the random variable X has a Rayleigh distribution with shape parameter σ. The probability density function (X > 0) is:
![]()
Where e is Euler’s number.
As the shape parameter increases, the distribution gets wider and flatter.
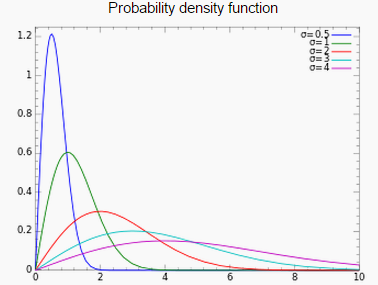
The distribution is widely used:
- In communications theory, to model multiple paths of dense scattered signals reaching a receiver.
- In the physical sciences to model wind speed, wave heights and sound/light radiation.
- In engineering, to measure the lifetime of an object, where the lifetime depends on the object’s age. For example: resistors, transformers, and capacitors in aircraft radar sets.1
- In medical imaging science, to model noise variance in magnetic resonance imaging.
Variance and Mean (Expected Value) of a Rayleigh Distribution
The expected value (the mean) of a Rayleigh is:
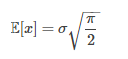
How this equation is derived involves solving an integral, using calculus:
The expected value of a probability distribution is:
E(x) = ∫ xf(x)dx.
Substituting in the Rayleigh probability density function, this becomes the improper integral:
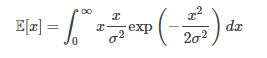
Where:
- exp is the exponential function,
- dx is the differential operator.
Solving the integral for you gives the Rayleigh expected value of σ √(π/2)
The variance of a Rayleigh distribution is derived in a similar way, giving the variance formula of:
Var(x) = σ2((4 – π)/2).
References
:
A 3-Component Mixture: Properties and Estimation in Bayesian Framework. Aslam et. al. Retrieved October 3, 2015. Available here.