What is a Rate Parameter?
The term “rate parameter” can mean several different things, depending on the context. The most common use is to describe exponential distributions or event rates in Poisson processes.
Use In Exponential Distributions
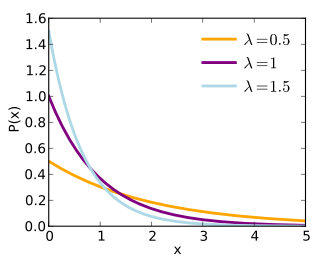
Perhaps the most common use is as an alternative to the scale parameter in some distributions (for example, the exponential distribution). It is defined as the reciprocal of the scale parameter and indicates how quickly decay of the exponential function occurs.
- When the rate parameter = 1, there is no decay.
- Values close to 1 (e.g. 0.8 or 0.9) indicate a slow decay.
- Values close to 0 (e.g. 0.1 or 0.2) indicate a steep decay.
The sign of the parameter gives its name to an exponential distribution; A negative exponential distribution has a negative rate parameter and vice-versa.
In a Poisson Process
The Poisson process has an event rate (sometimes called an intensity rate); Some authors will use the term rate parameter instead of the more common event rate. The event rate is the number of events per interval. For example, an emergency room might see 9 patients per hour, or a machine might produce 100 widgets per minute. The event rate is usually denoted by &lamdba;, although α is sometimes used (as in Devore, 2011).
Other Meanings
- Sometimes the term “rate parameter” is used as an alternative to “probability rate” but this is fairly uncommon.
References:
Devore, J. (2011). Probability and Statistics for Engineering and the Sciences. Cengage Learning.