Randomization in Statistics and Experimental Design

Design of Experiments > Randomization

What is Randomization?

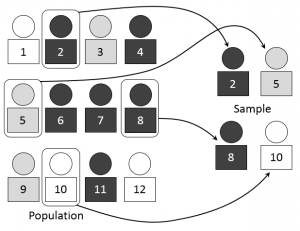
Randomization in an experiment is where you choose your experimental participants randomly. For example, you might use simple random sampling, where participants names are drawn randomly from a pool where everyone has an even probability of being chosen. You can also assign treatments randomly to participants, by assigning random numbers from a random number table.

If you use randomization in your experiments, you guard against bias. For example, selection bias (where some groups are underrepresented) is eliminated and accidental bias (where chance imbalances happen) is minimized. You can also run a variety of statistical tests on your data (to test your hypotheses) if your sample is random.

Randomization Techniques

The word “random” has a very specific meaning in statistics. Arbitrarily choosing names from a list might seem random, but it actually isn’t. Hidden biases (like a subconscious preference for English names, names that sound like friends, or names that roll off the tongue) means that what you think is a random selection probably isn’t. Because these biases are often hidden, or overlooked, specific randomization techniques have been developed for researchers:

1. Simple Random Sampling.

Simple Random Sampling is basically where you draw numbers from a hat, choose a card from a deck or a ball from a bingo machine. You can also assign numbers to participants, or treatments, and use a random number table to choose participants and treatment groups. It’s called simple random sample because it’s simple to implement. However, in practice, it’s tough to use because adequate sampling frames (lists of all possible participants) are sometimes difficult or impossible to find.


2. Permuted block randomization.
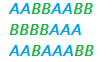Sometimes, just choosing participants randomly isn’t enough. You might want to balance your participants into groups, or blocks. Permuted block randomization is a way to randomly allocate a participant to a treatment group, while keeping a balance across treatment groups. Each “block” has a specified number of randomly ordered treatment assignments.

3. Stratified Random Sampling.

Stratified random sampling is used when your target population is split up into strata (characteristics like income level or housing status), and you want to include people from each strata. Once you’ve defined your strata, you can uses simple random sampling to choose elements from within each stratum. How this differs from permuted block randomization is that with PBR, you want to assign people into groups; With Stratified Random Sampling, your participants are already in groups, and you want to evenly sample from those groups.


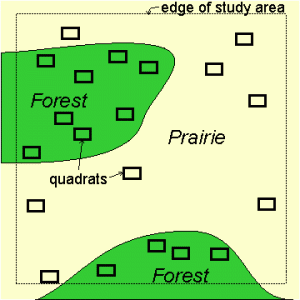
There are less popular randomization methods. You can find a full list of these sampling methods here: Types of Sampling.