Descriptive Statistics > Quadratic Mean / Root Mean Square
What is the Quadratic Mean / Root Mean Square?
The quadratic mean (also called the root mean square*) is a type of average. It measures the absolute magnitude of a set of numbers, and is calculated by:
- Squaring each number,
- Finding the mean of these squares,
- Taking the square root of that average.
If you label each element of your set as xi, where i is an index number numbering from 1 to n, the RMS can be described as:
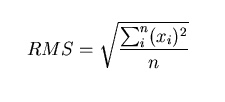
RMS gives a greater weight to larger items in a set and is always equal to or greater than the “regular” arithmetic mean (average).
Sometimes the quadratic mean is referred to as being “the same as” the standard deviation. This isn’t strictly true: standard deviation is actually equal to the quadratic deviations from the mean of the data set. For example, quadratic mean is used in the physical sciences as a synonym for standard deviation when referencing the “square root of the mean squared deviation of a signal from a given baseline or fit”(Wolfram).
The quadratic mean is also called the root mean square because it is the square root of the mean of the squares of the numbers in the set.
*Note: This is different from the root mean square error (RMSE), which is a value used in regression analysis to describe how spread out data is around a regression line.
Formula
The quadratic mean is equal to the square root of the mean of the squared values. The formula is:
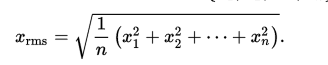
An equivalent formula has a summation sign (summation means “to add up”, so it’s telling you here to add all of the squared x-values up):
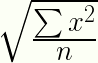
Examples of the Root Mean Square (RMS)
To find the root mean square of the set {1, 3, 4}:
- Square each of the numbers
- Find the mean of Step 1
- Find the square root of step 2
Worked Example
Find the Root Mean Square of 2, 4, 9, 10, and 12.
Step 1: Count the number of items.
N = 5.
Set this number aside for a moment.
Step 2: Square all of the numbers. 22,42,92,102, 122 = 4, 16, 81, 100, 144.
Step 3: Add the numbers from Step 2 up: 4 + 16 + 81 + 100 + 144 = 345.
Step 4: Divide Step 3 (the sum) by Step 1 (number of items in the set):
345/5 = 69.
Step 5: Find square root of Step 4. √(69) = 8.31.
That’s it!
The RMS of any series of positive identical numbers will be that same number, just as the average of a series of identical numbers is the number itself. The RMS of a series of negative identical numbers will be the absolute value of that number. For positive values, the RMS is either the same or a bit larger than the average.
Applications of RMS
RMS is important in many branches of physics, chemistry and engineering, and is a component of mathematical statistics. It can be used to measure the fit of an estimator to a data set.
RMS calculations play an especially important role in electrical engineering. For an arbitrary, periodic AC waveform the RMS voltage is given by:
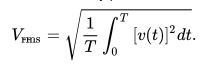
Root Mean Square is also used for very specialized purposes, such as the expression of average stand diameter in forestry. In this case, the quadratic mean of tree stand diameter is closer to the “true” mean of a sample of trees rather than the arithmetic mean.
RMS is also used anywhere where it’s the square of the values that matters, rather than the values themselves. For example, electrical current squared is proportional to power, so if you’re interested in total power (rather than current), this type of average is a good choice.
References
Gonick, L. (1993). The Cartoon Guide to Statistics Paperback – Illustrated. HarperPerennial.
Holmes, Susan. RMS. S60 Course Notes. Retrieved from http://statweb.stanford.edu/~susan/courses/s60/split/node49.html on November 20, 2018.
Kenney, J. F. and Keeping, E. S. “Root Mean Square.” §4.15 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 59-60, 1962.
Wolfram. Root Mean Square. Available at: http://mathworld.wolfram.com/Root-Mean-Square.html