The quadratic approximation is one way to approximate a curve. Quadratic polynomial approximations are specific examples of a useful class of quadratic approximations called Taylor polynomials.
The basic idea is that you want to approximate a function with a parabola.
General Form of Quadratic Approximation
The general form of a quadratic approximation is:
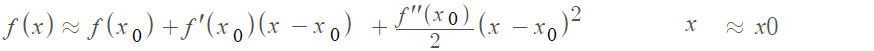
If it looks complicated, don’t worry: you don’t have to solve the equation; all you have to do is plug in some terms.
Let’s say you were trying to approximate a function at x = 1. The formula is basically saying to find three values at point x = 1 and add them up:
- f: The function at x = 1
- f′: The first derivative at x = 1
- f′′: The second derivative at x = 1.
Quadratic Approximation: Example
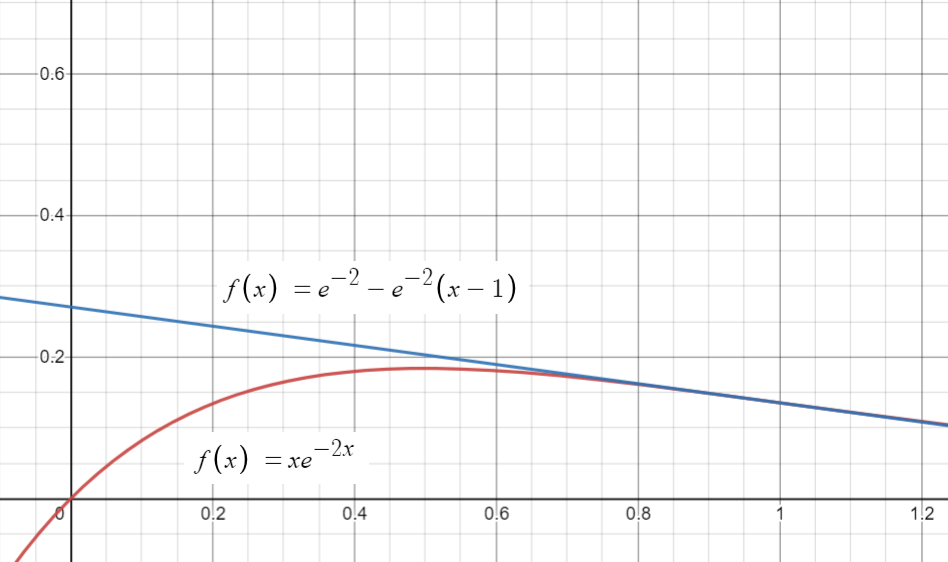
Example problem: Find the quadratic approximation for f(x) = xe-2x near x = 1
Step 1: Find the first derivative of the function. Use the product rule for this function (with x and e-2x) and then the chain rule (for e-2x):
f′(x) = e-2x – 2xe-2x = e-2x(1 – 2x).
Step 2: Find the second derivative of the function. In other words, find the derivative of the derivative you calculated in Step 1.
f′′(x) = -2e-2x – 2(e-2x – 2xe-2x)
= -4e-2x + 4xe-2x
= -4e-2x(1 – x).
Step 3: Find values at x = 1 for the function, and the first and second derivatives you calculated in Steps 1 and 2:
- f(1) = (1)e-2(1) = e-2
- f′(1) = e-2(1)(1 – 2(1)) = -e-2
- f′′(1) = -4(1)-2(1)(1 – (1)) = 0.
Step 4: Take the three values you calculated in Step 3 and insert them into the general formula . Note that the second derivative (from Step 3) was zero, so we can ignore the third part of the formula:
f(x) ≈ f(1) + f′(1)(x – 1)
≈ e-2 – e – 2(x – 1).
That’s it!
Use of Quadratic Approximation
In addition to modeling functions, approximations are used to:
- Study asymptotic behavior,
- Evaluate definite integrals (i.e. integrals that have a defined starting and stopping point),
- Understanding the growth of functions,
- Solve differential equations.
Next: How to use Taylor polynomials to approximate a function.