A probability vector is a vector (i.e. a matrix with a single column or row) where all the entries are non-negative and add up to exactly one. It’s sometimes also called a stochastic vector.

It’s not always so symmetric; in fact, it usually isn’t. For example, the stochastic vector representing the likelihood it might rain, snow, be cloudy without rain/snow, or be sunny all day might be (0.5, 0, 0.40, 0.10). Notice that here the entries still add up to one, and the categories represent all possible outcomes, and don’t overlap.
In essence, an n-dimensional probability vector may represent the probability distribution of a set of n variables. It’s a concise, very convenient way to represent the probability distribution of discrete random variables.
Probability Vector Properties
Every n-dimensional probability vector has a mean of 1/n.
The length of a probability vector is calculated with the formula:
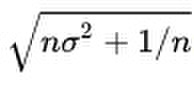 .
.
Here σ2 is the variance of all the entries in the probability vector. The ‘length’ of a probability vector, so defined, has nothing at all to do with the number of entries in the matrix.
- The longest possible probability vector has the value of 1 as one entry, and 0 in all others. It has a length of 1. In a situation with four possible alternatives (like the weather example above), the longest possible probability vector would be {1000} (or {0100}, or {0010}, or {0001}).
- The shortest possible probability vector has 1/n as each entry, and it’s length is 1/ √(n). In the dice example with six possible alternatives, the shortest possible vector would be {1/n, 1/n, 1/n, 1/n, 1/n}.
So the shortest vector represents a system with minimum certainty, (any of the options are equally likely to come to pass) and the longest a system with maximum certainty (you know exactly what will happen). For example, if the weather vector is {1000}, then there’s 100% chance of rain.
If A is a regular stochastic matrix, and is n x n, there is a unique stochastic vector v for which Av = v.
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Silva, G. (2007). Probability vect., Markov chains, stochastic matrix
Retrieved from https://www.dcce.ibilce.unesp.br/~gsilva/math152/Ch4-9-lay-classnotes.pdf on January 11, 2018
Quinlan, R. (2006). MA203 Course Notes Chapter 4: Markov Processes
Retrieved from http://www.maths.nuigalway.ie/~rquinlan/MA203/section4-1.pdf on January 11, 2018
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.