Integrals > Integral of Natural Log
Integral of Natural Log ln(x)
The general rule for the integral of natural log is:
Note: This is a different rule from the log rule for integration, which allows you to find integrals for functions like 1/x.
Example
Let’s say you had the basic function y = ln(x).
- Subtract “x” from the right side of the equation: y = ln(x) – x.
- Add “C”: y = ln(x) – x + C.
However, you’ll often be given more complicated functions to deal with.
More Complicated Integral of Natural Log Rules
Step 1: Check the following list for integration rules for more complicated integral of natural log rules. If you find your function there, follow the rule:

Step 2: Figure out if you have an equation that is the product of two functions. For example, ln(x)*ex. If that’s the case, you won’t be able to take the integral of natural log on its own, you’ll need to use integration by parts.
Tip: Sometimes you’ll have an integral with a natural log that you at first won’t recognize as a product of two functions, like ln⁄x. However, remember that you can rewrite division as multiplication. In this example, ln⁄x can be rewritten as 1⁄x * ln.
Integral of Natural Log: What is a Logarithm?
When you’re finding the integral of natural log, you’re dealing with (obviously) logarithms. A logarithm is the power to which a number is raised get another number. For example, take the equation 102 = 100; The superscript “2” here can be expressed as an exponent (102 = 100) or as a base 10 logarithm:
The base ten logarithm of 100 (written as log10 100) is 2, because 102 = 100.
Logarithms and exponents form a symbiotic relationship—basically, they “undo” each other. To put that another way,
logarithms are simply an exponent in a different form. For example logax = y is the same as ay = x.
Another way to think of the word log is that it’s a question. If you see the phrase log10 100, it’s asking “10 raised to what power equals 100?“. When you first start learning about logs, you’ll almost always start with learning about base 10 logs (i.e. multiples of 10 like 10*10 = 100 or 10*10*10 = 1,000); in other words, if you can multiply 10 by itself, you should pick up base 10 logs pretty quickly.
Examples in base 10:
- Log 10,000 = 4, because 103 = 10,000
- Log 1000 = 3, because 103 = 1000
- Log 100 = 2, because 102 = 100
- Log 10 = 1, because 101 = 10
Bases and Arguments
In a formula, the base is the subscript which you can find next to the letters log . The number following the subscript is called the argument; this is also called a power if you’re writing it in exponential form.
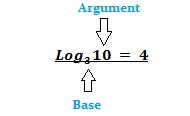
The base tells you the number you’re working with (i.e. the number that you’ll raise to some power). While you could technically have any number for a base, the three most common are:
- Base 10 (the decimal logarithm or common log). This is usually written as log(x),
- Base e; a special type of logarithm called a Natural Logarithm (e = Euler’s number, which is roughly equal to 2.718281828459),
- Base 2 (the binary logarithm).
If no base is written, you can usually assume base 10 (the “common logarithm”).
Base e
Natural logs are the inverse of ex, where “e” is Euler’s number. You can also think of natural logs as the time you need to reach a certain level of growth. For example, if your investment is showing 100% growth and you want to know when it will be ten times its size, you’d have to wait ln(10), or 2.302 years— assuming you have continuous compounding.
- Loge 5 = 1.6094379124, because e1.6094379124 = 5
- Loge 100 = 4.605170186, because e4.605170186 = 100
Properties of Logarithms
Some special properties of logarithms make them very easy to use in computation. Here are the basic logarithmic laws:
- logb mn = logbm + log bn
- logb(m/n )= logbm – logbn
- log b np = p logbn
- log b n = loga n logb a
Expanding Logarithmic Expressions: Examples
These simple steps work for any expression where there’s a “log” followed by a fraction with terms in the numerator and denominator; You don’t need to memorize any of the rules!.
Example question #1: Expand the following logarithmic expression:
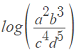
Step 1: Write “log” followed by all of the terms in the numerator (top) added together:
log (a2 + log b3)
Step 2: Write “log” followed by all of the terms in the denominator (bottom) added together:
log (c4 + log d5)
Step 3: Subtract Step 2 from Step 1:
log (a2 + log b3) – log (c4 + log d5)
Step 4: Remove the parentheses (multiply through):
log a23 – log c4 – log d5.
Step 5: Move each exponent to the front of each “log”:
Solution: 2 log a + 3 log – 4 log c – 5 log d.
Example question #2: Expand the following logarithmic expression:
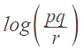
Step 1: Write “log” followed by all of the terms in the numerator (top) added together:
log (p + q)
Step 2: Write “log” followed by all of the terms in the denominator (bottom) added together:
log (r)
Step 3: Subtract Step 2 from Step 1:
log (p + q) – log (r)
Step 4: Remove the parentheses (multiply through):
log p + log q – log r.
Step 5: Move each exponent to the front of each “log”. The exponent here is “1” (it’s not normally written), so we can ignore this step:
Solution: log p + log q – log r.
Logarithmic vs. Exponential Formulas
If you find something like logax = y then it is a logarithmic problem. Always remember logarithmic problems are always denoted by letters “log”. If the calculation is in exponential format then the variable is denoted with a power, like x2 or a7.
- Logarithmic formula example: logax = y
- Exponential formula example: ay = x
Index Calculus
Index calculus (or more precisely, index calculus algorithm) is an algorithmic technique to compute indices (discrete logarithms). It’s heavily used in cryptography and number theory.
History of Index Calculus
Although index calculus had been known to number theorists since Belgian mathematician’s Maurice Kraitchik’s groundbreaking work in the 1920s (Kraitchik, 1926/1929), it wasn’t until the 1970s that it was rediscovered by mathematicians including Adleman (1979) who optimized the technique for cryptography (Ryabko & Fionov, 2005). Within the field of cryptography, the algorithm is sometimes referred to as Adleman’s index calculus algorithm.
Integral of Natural Log: References
Abramowitz, M. and Stegun, I. A. (Eds.). “Logarithmic Function.” §4.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 67-69, 2003.
Adleman, L. (1979). A subexponential algorithm for the discrete logarithm problem with applications to cryptography. SFCS ’79: Proceedings of the 20th Annual Symposium on Foundations of Computer ScienceOctober 1979 Pages 55–60https://doi.org/10.1109/SFCS.1979.2
Beyer, W. H. “Logarithms.” CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 159-160 and 221, 1987.
Conway, J. H. and Guy, R. K. “Logarithms.” The Book of Numbers. New York: Springer-Verlag, pp. 248-252, 1996.
Jacobsen M. & Williams, H. (2009). Solving the Pell Equation. Springer.
Joux, A. (2009). Algorithmic Cryptanalysis. CRC Press.
Kraitchik, M. (1926). Theorie des Nombres, Tome II.
Kraitchik, M. (1929). Recherches sur la Th´eorie des Nombres, Tome II.
Math Review: Useful Math for Everyone. Section 4. What is a Logarithm? Retrieved from http://www.mclph.umn.edu/mathrefresh/logs.html on December 8, 2018.
Nau, R. The logarithm transformation. Retrieved 3/11/2020 from: https://people.duke.edu/~rnau/411log.htm
Pappas, T. “Earthquakes and Logarithms.” The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 20-21, 1989.
Ryabko, B. & Fionov, A. (2005). Basics of Contemporary Cryptography for IT Practitioners. World Scientific.