Probability > Prior Probability: Uniformative, Conjugate
What is Prior Probability?
Prior probability is a probability distribution that expresses established beliefs about an event before (i.e. prior to) new evidence is taken into account. When the new evidence is used to create a new distribution, that new distribution is called posterior probability. In some ways, it’s just an educated guess (i.e. an ansatz) to start off the process of finding a solution. 
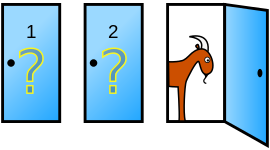For example, you’re on a quiz show with three doors. A car is behind one door, while the other two doors have goats. You have a 1/3 chance of winning the car. This is the prior probability. Your host opens door C to reveal a goat. Since doors A and B are the only candidates for the car, the probability has increased to 1/2. The prior probability of 1/3 has now been adjusted to 1/2, which is a posterior probability.
In order to carry our Bayesian inference, you must have a prior probability distribution. How you choose a prior is dependent on what type of information you’re working with. For example, if you want to predict the temperature tomorrow, a good prior distribution might be a normal distribution with this month’s mean temperature and variance.
Uninformative Priors
An uninformative prior gives you vague information about probabilities. It’s usually used when you don’t have a suitable prior distribution available. However, you could choose to use an uninformative prior if you don’t want it to affect your results too much. The uninformative prior isn’t really “uninformative,” because any probability distribution will have some information. However, it will have little impact on the posterior distribution because it makes minimal assumptions about the model. For the temperature example, you could use a uniform distribution for your prior, with the minimum values at the record low for tomorrow and the record high for the maximum.
Conjugate prior distribution
A conjugate prior distribution (or just conjugate prior) is a prior distribution which — along with the data model — produces a posterior distribution that shares the same functional form as the prior distribution, but with new and updated parameter values [1]. In other words, if the prior distribution and the posterior distribution are members of the same parametric family, then the prior is a conjugate for the likelihood function.
References
[1] Hitchcok, D. STAT 535: Chapter 5: More Conjugate Priors. Retrieved August 20, 2023 from: https://people.stat.sc.edu/hitchcock/stat535slides5BRBhandout.pdf