Statistics Definitions > Power Law
What is the Power Law?
The power law (also called the scaling law) states that a relative change in one quantity results in a proportional relative change in another. The simplest example of the law in action is a square; if you double the length of a side (say, from 2 to 4 inches) then the area will quadruple (from 4 to 16 inches squared). A power law distribution has the form Y = k Xα, where:
- X and Y are variables of interest,
- α is the law’s exponent,
- k is a constant.
Any inverse relationship like Y = X-1 is also a power law, because a change in one quantity results in a negative change in another.
Examples
The power law can be used to describe a phenomenon where a small number of items is clustered at the top of a distribution (or at the bottom), taking up 95% of the resources. In other words, it implies a small amount of occurrences is common, while larger occurrences are rare. For example, where the distribution of income is concerned, there are very few billionaires; the bulk of the population holds very modest nest eggs.
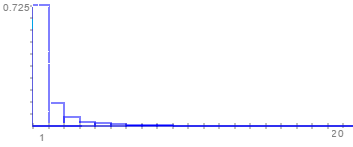
Other examples of phenomena with this type of distribution:
- Distribution of income,
- Magnitude of earthquakes,
- Size of cities according to population,
- Size of corporations,
- Trading volumes on the stock market,
- word frequencies.
If you plot two quantities against each other with logarithmic axes and they show a linear relationship, this indicates that the two quantities have a power law distribution.
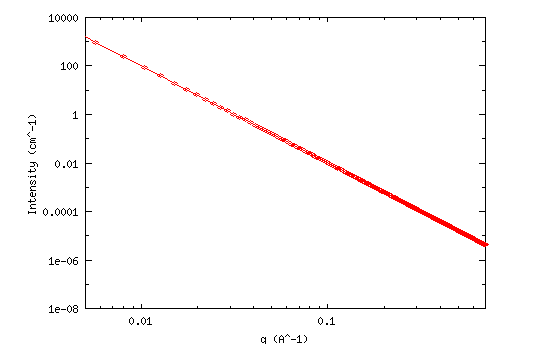
Similar Distributions and Laws
A special type of the this type of distribution is the Pareto Principle (also called the Pareto Law), which is an unscientific “law” that states 80% of effects come from 20% of causes. In other words, most of what we do has little effect.
A related law is Zipf’s law which usually refers to the frequency of an event relative to its rank. Zipf’s law states that, given a list of the most frequent words in an arbitrary book, the most frequent word will appear twice as often as the second most frequent word, which will appear twice as often as the third most frequent, and so on. In its simplest form, Zipf’s law is equal to the power law. Zipf’s law gives rise to the Zeta Distribution.
Reference:
Barker, J. (1999). Power Law. Retrieved 7-15-2015 from : https://www.ncnr.nist.gov/resources/sansmodels/PowerLaw.html.