Statistics Definitions > Pascal’s Triangle
Pascal’s Triangle is a number pattern in the shape of a (not surprisingly!) a triangle. It is named after the French mathematician Blaise Pascal. Pascal’s Triangle has many applications in mathematics and statistics, including it’s ability to help you calculate combinations.
Row 0 1 Row 1 1 1 Row 2 1 2 1 Row 3 1 3 3 1 Row 4 1 4 6 4 1 Row 5 1 5 10 10 5 1 Row 6 1 6 15 20 15 6 1 Row 7 1 7 21 35 35 21 7 1
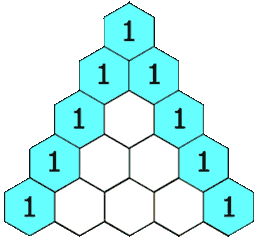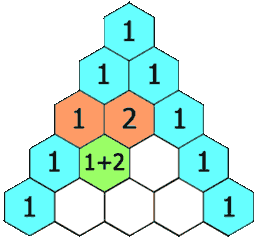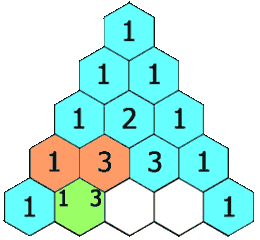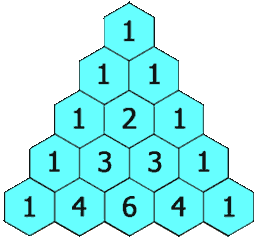
Each number in the triangle is the sum of the two numbers above it. For example, there’s a
in the center of row 4: it’s the sum of 3 and 3 in the row above. The very first and very last number in any row are always going to be 1.
How to find combinations with Pascal’s Triangle
Pascal’s Triangle can be used to find combinations. The top row in Pascal’s Triangle is row zero, and the first item in any row (the 1s) are item zero in that row. For example, let’s sat we wanted to find 6_C_4. Look in Row 6, at item number 4. the answer is 15.
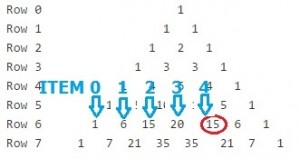
Other Uses
Outside of probability, Pascal’s Triangle is also used for:
- Algebra, where coefficient of polynomials can be used to find the numbers in Pascal’s triangle. Algebra is outside the scope of this site, but you can find an excellent explanation of this concept on the Dr. Math website.
- Finding triangular numbers (1, 3, 6, 10, 15, 21, 28, 36, 45, …). Triangular numbers are the “dots” that make up a triangle. For example, you can make a very simple triangle from 3 dots, one at each corner angle. For more on triangular numbers, check out Math is Fun.
There are many, many other interesting patterns you can find in the triangle, including prime numbers, Catalan numbers, and the Fibonacci sequence. J Wilson’s page on the University of Georgia website has an excellent rundown of many number patterns that are hidden in Pascal’s Triangle.
Check out our YouTube channel for hundreds of statistics help videos!