Statistics Definitions > Parametric Modeling
What is Parametric Modeling?
Parametric modeling is creating a model from some known facts about a population. These “facts” are called parameters, (hence the name parametric). While it’s used in statistics, parametric modeling is also a specialized field in mechanical design or building design.
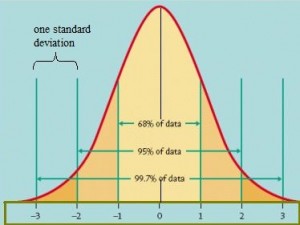
The normal distribution is a simple example of a parametric model. The parameters used are the mean(μ) and standard deviation(σ). The standard normal distribution has a mean of 0 and a standard deviation of 1.
Other distributions that can be used for parametric modeling include:
- The Weibull distribution, which has the parameters λ, α and μ.
- The Poisson distribution, which has a single parameter, λ.
Parametric vs. Nonparametric Modeling
In order to make predictions using a parametric model, all you need to know is the model’s parameters. For example, if you know the mean and standard deviation for a normal model, you can predict where a future data item will fall. These models succinctly capture aspects about the real world and are efficient ways to model past and future trends.
The opposite of a parametric model is a non-parametric model. With a non-parametric model, you have more subtle information about the model, and there many be many, many, different inputs. Predictions with these models tend to be less accurate, and larger data sets may be costly and inefficient to process.
Parametric Modeling in MCAD
MCAD software uses parameters. However, the word parameter here means something slightly different than with a statistical parameter. A statistical parameter is a fact about the population (like the average height, the median weight, or the spread of data about the mean); with MCAD, the parameters are dimensions which drive the geometry of the model.. If you change a dimension in the model (i.e. change a parameter), the model size will change. A Few examples of parameters used in modeling:
- Material density formulas.
- Dimensions to create model features.
- Data that describes a reference surface.
For example, a reference surface could describe an endcap on a pipe. When you create the model, the pipe is automatically placed at the end of the pipe, no matter what changes you make to the pipe’s length.