Contents:
- What is a Normalized Function?
- Why”Normalized”?
- How to Get The Normalized Function
- About Normalized Data
- Normalization vs. Standardization
What is a Normalized Function?
A normalized function is one where the integral is equal to 1 over the entire domain. Mathematically, it is defined as (Miller, 2006):
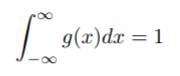
Where g(x) is defined on the interval -∞ to ∞.
Why “Normalized”?
Normalization can have many meanings in math, but generally it involves setting lengths to 1. For example:
- When you normalize a vector, you set the length to 1.
- When rescaling data, you set the data values to fall between 0 and 1.
- With a normalized function you set the integral to equal 1.
How to Get The Normalized Function
Some functions are already normalized. For example, the Dirac delta function is normalized. Other functions can be normalized by finding the norm. Watch the video for an example of how to find the normalization factor:
Köthe (2012) defines a normalized function as a function h(c) having bounded variation on [0,1] with h(0) = 0 and h(c) = h(c + 0) for 0 < c < 1. Using this definition, you can get the normalized function g*(c) for some arbitrary function g(c) of bounded variation by setting:
- g*(0) = 0,
- g*(1) = g(1) – g(0) and
- g*(c) = g(c + 0) – g(c) for 0 < c < 1.
About Normalized Data
Thhe term normalized data can have multiple meanings. In most cases, when you normalize data you eliminate the units of measurement, enabling you to more easily compare data from different places. Some of the more common ways to normalize data include:
- Transforming statistical data using a z-score or t-score. This is usually called standardization. In the vast majority of cases, if a statistics textbook is talking about normalizing data, then this is the definition of “normalization” they are probably using.
- Rescaling data to have values between 0 and 1. This is usually called feature scaling. One possible formula to achieve this is:
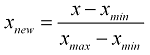
- Standardizing residuals: Ratios used in regression analysis can force residuals into the shape of a bell curve.
- Normalizing Moments using the formula μ/σ.
- Normalizing vectors (in linear algebra) to a norm of one. Normalization in this sense means to transform a vector so that it has a length of one.
This list is by not means all-inclusive. I’ve included the most common ones, but be aware there are many, many other meanings for the word normalization.
Normalization vs. Standardization
The terms normalization and standardization are sometimes used interchangeably, but they usually refer to different things. Normalization usually means to scale a variable to have values between 0 and 1, while standardization transforms data to have a mean of zero and a standard deviation of 1. This standardization is called a z-score, and data points can be standardized with the following formula:
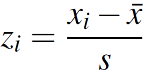
Where:
- xi is a data point (x1, x2…xn).
- x̄ is the sample mean.
- s is the sample standard deviation.
Z-scores are very common in statistics. They allow you to compare different sets of data and to find probabilities for sets of data using standardized tables (called z-tables).
Normalized Function: References
Köthe, G. (2012). Topological Vector Spaces. Springer.
Khrennikov, A. (2009). Interpretations of Probability. Walter De Gruyter.
Miller, W. (2006). Delta Functions exercise solutions. Retrieved January 24, 2021 from: http://www.cchem.berkeley.edu/chem120a/extra/delta_functions_sol.pdf
R Documentation. Normalized Function. Retrieved January 24, 2021 from: https://www.rdocumentation.org/packages/DAPAR/versions/1.4.7/topics/normalizeD