Probability and Statistics > Probability > Normal Probability Practice Problems
These normal probability practice problems will help you practice calculating z-scores and using the z-table.
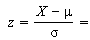
General steps for solving normal probability practice problems:
- Use the equation above to find a z-score. If you don’t know how to look up z-scores (or if you want more practice, see this z-score article for videos and step-by-step instructions.
- Look up the z-score in the z-table and find the area.
- Convert the area to a percentage.
If you more need help with these steps, see the normal distribution word problems index, which outlines the steps in detail (with videos).
Normal Probability Practice Problems.
Click on the question for the answer!
1. Scores on a particular test are normally distributed with a standard deviation of 4 and a mean of 30. What is the probability of anyone scoring less than 40?
- z = 40-30/4 = 2.5. Area to the left of 2.5 =.9938.
2. Annual salaries for a large company are approximately normally distributed with a mean of $50,000 and a of $20,000. What percentage of company workers may under $40,000?
- z = 40000-50000/20000 = -.5 = .3085 = 30.85%.
3. IQ scores have a normal distribution with a mean of 100 and a standard deviation of 15. What percent of people have an IQ above 120?
- z = (120-100)/15 = 1.33 = 1 – 0.9082 = 0.0918 (9.18%).
4. The amount of time a student taking statistics spends on studying for a test is normally distributed. If the average time spent studying is 12 hours and the standard deviation is 4 hours, what is the probability that a student will spend more than 8 hours studying?
- z = (8-12) / 4 = 1 – .1587 = 0.8413 = 84.13%
5. The amount of candy dispensed by a candy machine is normally distributed with a mean of 0.9 oz and a standard deviation of 0.1 ounces. If the machine is used 500 times, how many times will it dispense more than 1 oz of candy?
- First, find the probability of more than 1 oz candy being dispensed: z = 1 – 0.9 / 0.1 = 1 = .8413. The area greater than this (to the right of the z-score) is 1 – .8413 = 0.1587. Finally, find 15.87% of 500 = 79.35 (rounded down that’s 79 times out of 500).
Check out our YouTube channel for more stats help and tips!