You may want to read this article first: What is the Studentized Range?
Newman-Keuls (sometimes called Student–Newman–Keuls or SNK) is a post hoc test for differences in means. Once an ANOVA has given a statistically significant result, you can run a Newman-Keuls to see which specific pairs of means are different. The test is based on the studentized range distribution.
A variant of the Student–Newman–Keuls test is Duncan’s multiple range test (MRT), which uses increasing alpha levels to calculate critical values in each step of the procedure. This results in a lower probability of Type I error.
Note: This test has a lower power than ANOVA. Therefore you should only run it if an ANOVA finds a significant result. That said, if the ANOVA finds an overall significant difference but the SNK fails to find significance differences between any pair, it’s possible that the lower power has resulted in a failure to find which pairs are significant. If this happens, run an alternate post hoc test like Tukey’s HSD or Duncan’s MRT.
How the Test Works
The basic null hypotheses for the test are:
- Ho: mean A = mean B,
- Ha: mean A ≠ mean B.
Where A and B could be any possible pair.
This test is usually performed with software. It works like most other hypothesis tests: calculate a test value, find the critical value, and compare the two. By hand, you’ll need to perform several calculations:
Step 1: Order means from largest to smallest.
The next steps are to compare differences between the group with the largest mean to the group with the smallest mean:
Step 2: Calculate the standard error using the mean squared error (from ANOVA output). If the sample sizes are equal, use formula 1. If they are not equal, use formula 2.
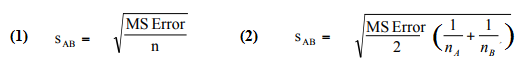
Step 3: Calculate the q-value using the following formula:
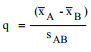
Step 4: Find the q critical value from the q critical value table. The rows are the number of means being compared (i.e. the number of treatments) and the columns are the degrees of freedom.
Step 5: Compare the calculated value (Step 3) with the table value (Step 4). If the calculated value is greater than the table value then reject the null hypothesis that the two means are equal (i.e. the means are therefore not equal). If the calculated value is lower than the table value then the null hypothesis stands that the two means are equal.
If the two means are equal, stop the test. You can conclude that there is no difference between any pairs of means.
If the two means are unequal, repeat Steps 2 through 5 for the next highest mean and the lowest mean. Stop when you find a pair of means that are equal.
Newman-Keuls vs. Tukey HSD
The Newman-Keuls and Tukey HSD work with different distributions (Tukey’s with the t-distribution and Newman-Keuls with the studentized range) but that doesn’t necessarily mean that one is better than the other. In fact, there’s no consensus on how to choose between the two. Although the N-K test was designed to have more power than Tukey’s HSD, the probability of making a Type I error can’t be calculated for the N-K test, nor is it possible to calculate confidence intervals around difference between means. An oft-cited problem with SNK is that once you start comparing more than four means, the familywise error rate increases to unacceptable levels (e.g. .15 for 5 means). In reality, it’s extremely rare to have an experiment where you actually think five or more sets of means are completely equal, but if this unusual situation is true you may want to select a different post hoc test.
References:
Herve´ Abdi · Lynne J. Williams. Newman-Keuls Test and Tukey Test. In Neil Salkind (Ed.), Encyclopedia of Research Design. Thousand Oaks, CA: Sage. 2010