Probability > Mutually Inclusive
Mutually inclusive events have some overlap with each other. For example, the events “buying an alarm system” and “buying bucket seats” are mutually inclusive, as both events can happen at the same time. In other words, a car buyer can opt to buy and alarm and bucket seats. On a Venn diagram, this overlap is shown as an intersection of two circles:
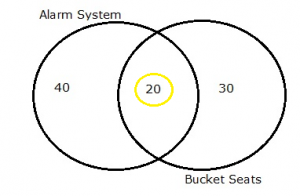
On the other hand, mutually exclusive events can’t happen at the same time. For example, you can’t get a car with bucket seats and regular seats; you have to choose one option or the other.
A series of options that go hand in hand can be mutually inclusive: driving a car and having a driver’s license; having electricity at your home and paying the electric bill; working as a programmer and knowing how to use a computer. Another way to think of it is that two mutually inclusive events cannot happen independently. If you have two events that are dependent in some way, they are mutually inclusive.
In probability terms, two events are mutually inclusive if their intersection is greater than zero:
P(A or B) > 0.
Figuring out Mutually Inclusive Probability.
For any two events A and B:
P(A or B) = P(A) + P(B) – P(A and B).
Sample Question: if you choose a card from a standard deck of cards, what is the probability of getting a queen or a heart?
It’s possible to get a queen and a heart when choosing a card from a deck of cards. The queen of hearts is the intersection P(A and B), so:
P(Getting a queen or Getting a heart) = P(queen) + P(heart) – P(queen of hearts) =
4/52 + 13/52 – 1/52 = 16/52.
This is called the addition rule. It can be used to calculate probabilities for both mutually exclusive and mutually inclusive events. In the case of mutually exclusive events, the intersection P(A and B) is zero.
Next: The Addition Rule.