Descriptive Statistics > Measures of Variation
Variation is a way to show how data is dispersed, or spread out. Several measures of variation are used in statistics.
Different Measures of Variation
The Range
A range is one of the most basic measures of variation. It is the difference between the smallest data item in the set and the largest. For example, the range of 73, 79, 84, 87, 88, 91, and 94 is 21, because 94 – 73 is 21.
Quartiles
Quartiles divide your data into quarters: the lowest 25%, the next lowest 25%, the second highest 25% and the highest 25%.
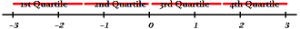
Interquartile Range
The interquartile range is one of the most popular measures of variation used in statistics. It is a measure of how data is spread around the mean. The basic formula is:
IQR = Q3 – Q1
For more detail, see: Interquartile range in statistics: What it is and How to find it.
Variance
Variance tells you how far a data set is spread out, but it is an abstract number that really is only useful for calculating the Standard Deviation.
This video shows you how to find both:
Sum of Squares
Sum of squares is a fairly advanced technique that measures how data varies around a central number, like the mean. It’s used extensively in regression analysis to calculate how well data points correspond to a line of best fit. For more on how to calculate it, see: Sum of Squares.
Empirical Rule
How much of data lies a certain distance from the mean? If you have a normal distribution, the empirical rule can tell you this. For example:
- About 68% of results will fall between +1 and -1 standard deviations from the mean.
- About 95% will fall between +2 and -2 standard deviations.
If you have another (non-normal) distribution, you can still calculate these percentages, using Chebyshev’s Theorem.