F Ratio > Mean Square Between
What is Mean Square Between?
Mean square between gives you an idea of differences between sample means. It’s biggest use is to find the F ratio in an ANOVA test. Depending on the author, it is denoted by MS(B), σ2 or ![]() .
.
On its own, MS(B)isn’t a very useful statistic. Unlike the mean or standard deviation, you can’t use it for straightforward comparisons. However, if the mean squared error (MSE) and MS(B) are roughly equal, this is a good indication that your population means are equal. If the population means are equal, then MS(B) can be used to estimate the variance, σ2. If the population means are not equal, then MS(B) will overestimate σ2.
Usage
Mean square between is used to calculate the F ratio (sometimes called the F-value):
F Ratio = MSB/MSE.
For small samples, the F ratio may not be helpful. But for larger samples, MSB and MSE are usually equal and so would return an F ratio of 1. Large F ratios (over 2 or so) indicate that the population means are not equal.
MS(B) is also used to calculate the total sum of squares, which is equal to the sum of within mean square and between mean square.
Sum of Squares SS = Within Mean Square MS(W) + Mean Square Between MS(B)
In general, smaller sample means result in smaller values for MS(B).
Formula
MS(B) is calculated from the sample means (compared to MSE, which is calculated from sample variances). To find MS(B), divide the between group variation (SSbetween) divided by between group degrees of freedom (k-1). As a formula, that’s:
MS(B) = SSbetween / (k-1)
Alternatively, you can multiply n (the sample size) by the variance of the sampling distribution of the mean:
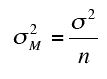
For example, if the variance for the sample means is 0.199 and your sample size is 39, then MS(B) = 0.199*39 = 38.61.