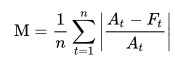The mean absolute percentage error (MAPE) — also called the mean absolute percentage deviation (MAPD) — measures accuracy of a forecast system. It measures this accuracy as a percentage, and can be calculated as the average absolute percent error for each time period minus actual values divided by actual values.
The mean absolute percentage error (MAPE) is the most common measure used to forecast error, probably because the variable’s units are scaled to percentage units, which makes it easier to understand [1]. It works best if there are no extremes to the data (and no zeros). It is often used as a loss function in regression analysis and model evaluation.
Formula for Mean Absolute Percentage Error
- n is the number of fitted points,
- At is the actual value,
- Ft is the forecast value.
- Σ is summation notation (the absolute value is summed for every forecasted point in time).
Percentage errors are calculated in terms of absolute errors, without regards to sign. This avoids the problem of positive and negative errors canceling each other out [2].
References
[1] MAPE (Mean Absolute Percentage Error. Working with Planning. Retrieved May 27, 2022 from: https://docs.oracle.com/en/cloud/saas/planning-budgeting-cloud/pfusu/insights_metrics_MAPE.html
[2] (2000) MEAN ABSOLUTE PERCENTAGE ERROR (MAPE). In: Swamidass P.M. (eds) Encyclopedia of Production and Manufacturing Management. Springer, Boston, MA . https://doi.org/10.1007/1-4020-0612-8_580