Contents:
- What is the Mann Whitney Test?
- Null Hypothesis
- Direct Method
- Assumptions
- How to run a Mann Whitney Test in SPSS (Video)
What is a Mann Whitney U Test?
The Mann-Whitney U test is the nonparametric equivalent of the two sample t-test. While the t-test makes an assumption about the distribution of a population (i.e. that the sample came from a t-distributed population), the Mann Whitney U Test makes no such assumption.
Null Hypothesis for the Test
The test compares two populations. The null hypothesis for the test is that the probability is 50% that a randomly drawn member of the first population will exceed a member of the second population.
Another option for the null hypothesis is that the two samples come from the same population (i.e. that they both have the same median).
The result of performing a Mann Whitney U Test is a U Statistic. For small samples, use the direct method (see below) to find the U statistic; For larger samples, a formula is necessary. Or, you can use technology like SPSS to run the test.
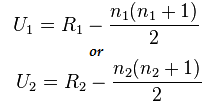
Mann Whitney U Test Direct Method
This method is limited only by how much computation you want to perform. The larger the sample, the more complex the math:
- Name the sample with the smaller ranks “sample 1” and the sample with the larger ranks “sample 2”. Choosing the sample with the smaller ranks to be “sample 1” is optional, but it makes the computation easier.
- Take the first observation in sample 1. Count how many observations in sample 2 are smaller than it. If the observations are equal, count it as one half. For example, if you have ten that are less and two that are equal: 10 + 2(1/2) = 11.
- Repeat Step 2 for all observations in sample 1.
- Add up all of your totals from Steps 2 and 3. This is the U statistic.
Assumptions for the Mann Whitney U Test
- The dependent variable should be measured on an ordinal scale or a continuous scale.
- The independent variable should be two independent, categorical groups.
- Observations should be independent. In other words, there should be no relationship between the two groups or within each group.
- Observations are not normally distributed. However, they should follow the same shape (i.e. both are bell-shaped and skewed left).
How to Run a Mann Whitney Test in SPSS
Watch the video for the steps: