
A long tail distribution has tails that taper off gradually rather than drop off sharply. They are a subset of heavy-tailed distributions. It’s easy to visualize the idea of a long tailed function, and slightly harder to make it concrete.
If we want to be rigorous, though, there is a exact mathematical definition of a long tailed function (Foss et. al, 2013):
A (ultimately positive) function f is defined according to a limit —a term introduced in calculus. Very basically, the limit tells you where the distribution converges to at a certain point. In this case, if the ratio of x + y and x converge to 1 as the x-values get much larger, then the distribution is long-tailed:
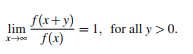
Derivatives of the Long Tail Distribution
The long tailed property of distributions carries over into many derivative distributions.
If f1, f2… fn are all long tailed, then:
Any distribution that can be expressed as a product of these, fx= f1 · f2… · fn is also long tailed.
Any distribution that can be expressed as a linear combination of these is long tailed. That means that any function
![]()
is long tailed, where c1, c2… cn may be any positive non constant.
Applications of a Long Tail Distribution
Commerce and marketing schemes often find that there sales can best be modeled by long tail distributions. For instance, an internet store may have certain items with very high sales (modeled by the center of the distribution curve) and a large number of items with much lower sales (modeled by the long tail).
Although the sales volume for every individual item in the tail may be negligible, there are enough items that they play a significant role in the general profit taking. In fact, the profit from low-sale volume items can rival or even sometimes leave in the dust the profit made from best-sellers—provided only the tail is long enough.
References
Foss et. al (2013). Heavy Tailed and Long Tailed. Retrieved December 26 2013 from: http://www.springer.com/cda/content/document/cda_downloaddocument/9781461471004-c1.pdf?SGWID=0-0-45-1395304-p175250259
Goel, A. (2009). Long Tail: The Lecture. Retrieved December 26, 2017 from: https://web.stanford.edu/~ashishg/msande235/spr08_09/Lecture07.pdf