Probability Distributions > Lindley Distribution
What is a Lindley Distribution?
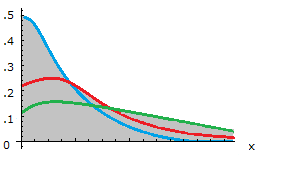The Lindley distribution is an important tool for describing the lifetime of processes and devices across a range of fields such as biology, engineering, and medicine. In fact, it’s proven to be particularly effective in modeling mortality studies. This distribution is characterized by a shape parameter, θ, which can result in either unimodal or consistently decreasing distributions. The Lindley distribution is known for having thin tails, meaning that the distribution decreases exponentially for large values of x. It’s worth noting that the term “Lindley-Exponential Distribution” refers to the generalized form of this important distribution.
PDF and CDF
The probability density function of a random variable X in a Lindley distribution with parameter θ is:
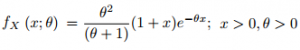
The cumulative distribution function for the one-parameter function is:
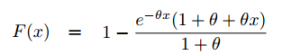
Types
Many forms of the distribution have been described in academic literature, including:
- A two-parameter form (Shanker et. al),
- A two-parameter weighted form (Ghitany et’ al),
- A generalized Poisson-Lindley (Mahmoudi et. al.),
- An extended (EL) distribution (Bakouch et. al),
- An exponential geometric distribution (Adankis and Loukas).
- The transmuted Lindley-Geometric Distribution (Merovci, and Elbatal)
Moments
Moments for the one-parameter distribution (from Shanker et. al):
Note that these moments are only valid for the one-parameter form. Other parameters will have different moments. For example, you can find moments for the Transmuted Lindley-Geometric distribution with the following:
If X has T LG (θ, x) ,φ = (θ, p,λ) then the rth moment of X is given by (from Merovci and Elbatal):
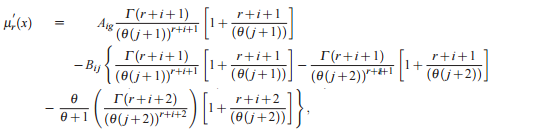
Where
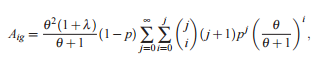
and
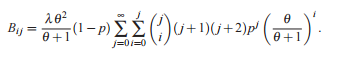
Related Distributions
Related distributions that model lifetimes:
References:
Adamidis K., and Loukas S.,(1998) A lifetime distribution with decreasing failure rate, Statistics and Probability Letters, Vol(39), 35-42.
Bakouch H. S., Al-Zahrani B. M., Al-Shomrani A. A., Marchi V. A., and Louzada F.,(2012)
An extended LD, Journal of the Korean Statistical Society, Vol(41), 75-85.
Bhati, D., and Malik, A.,(2014), On Lindley-Exponential Distribution: Properties and Application. Retrieved 8/24/2016 from https://arxiv.org/pdf/1406.3106.pdf.
Ghitany M. E., Alqallaf F., Al-Mutairi D. K., and Husain H. A., (2011) A two-parameter weighted Lindley distribution and its applications to survival data, Mathematics and Computers in Simulation, Vol. (81), no. 6,1190-1201.
Mahmoudi E., and Zakerzadeh H., (2010) Generalized Poisson Lindley , Communications in Statistics: Theory and Methods, Vol (39), 1785-1798.
Merovci, F., and Elbatal, I. (2014) Transmuted Lindley-Geometric Distribution and its Applications. Journal of Statistics Applications and Probability, 3, No. 1, 77-91 (20). Retrieved 8/24/2016 from http://naturalspublishing.com/files/published/e69vpy514e5z24.pdf.
Shanker R., Sharma S., and Shanker R., (2013) A Two-Parameter Lindley for
Modeling Waiting and Survival Times Data, Applied Mathematics, Vol (4), 363-368. Retrieved 8/24/2016 from here.
Shanker et. al (2015). On Modeling of Lifetimes Data Using Exponential and Lindley Distributions. Biometrics & Biostatistics International Journal. Volume 2 Issue 5.