Lilliefors Test for Normality & Exponential Distributions

Normality > Lilliefors Test

What is Lilliefors Test?

The Lilliefors test is a test for normality. It is an improvement on the Kolomogorov-Smirnov (K-S) test — correcting the K-S for small values at the tails of probability distributions — and is therefore sometimes called the K-S D test. Many statistical packages (like SPSS) combine the two tests as a “Lilliefors corrected” K-S test.

Unlike the K-S test, Lilliefors can be used when you don’t know the population mean or standard deviation. Essentially, the Lilliefors test is a K-S test that allows you to estimate these parameters from your sample.

Running the Test

• The null hypothesis (H₀) for the test is the data comes from a normal distribution.
• The alternate hypothesis (H₁) is that the data doesn’t come from a normal distribution.

The test assumes that you have a random sample.

If the test statistic is significantly large, you can reject the null hypothesis and conclude that the data is not normal.

Calculation Steps

The formulas involved in the Lilliefors test are quite time consuming (in part due to the fact that you have to calculate z-scores for every single sample member!), so the test is usually performed with software:

• Minitab: At the time of writing, Minitab doesn’t have an option for this test.
• In R: Use lillie.test in the package nortest.
• In SPSS (21.0.0.1 and later only), run the K-S test, click “Options” and specify normal. If you don’t enter the population mean and standard deviation, SPSS will automatically run Lilliefors. A footnote will appear in the output indicating that the correction was used.

The general steps that the test follows are:

1. Calculate X_i using this formula:
   
   
   Where:
   • Z_i = the individual z-scores for every member in your sample,
   • X_i = individual member / data point,
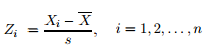
   • = sample mean,
     ,
2. Calculate the test statistic, which is the empirical distribution function (EDF) based on the Z_is. The formula is
   Where:
   F*(x) = the standard normal distribution function.

S(x) = the empirical distribution function of the z_i values.

3. Find the critical value for the test from this table and reject the null hypothesis if the test statistic T is greater than the critical value.

Cautions

Lilliefors test has a low power. According to R documentation, it is “known to perform worse” than either the Anderson-Darling or Cramer-von Mises tests.

Lilliefors test for Exponential Distribution

Lilliefors can also be used to test for a fit to an exponential distribution. The general steps are almost identical to the Lilliefors normality test, except with a couple of minor changes to the null hypothesis and formulas:

• The null hypothesis (H₀) for the test is the data comes from an exponential distribution.
• The alternate hypothesis (H₁) is that the data doesn’t come from an exponential distribution.

The test assumes that you have a random sample.

The software commands are almost the same, except you would specify exponential instead of normal:

1. In Matlab, specific exp in the Lilliefors command: h = lillietest([variable name],’Distr’,’exp‘). IF the test returns a 1, the data does not fit an exponential distribution.
2. In SPSS, click the “Options” button for the K-S test and choose exponential.

Reference:
IBM. K-S test of normality in NPAR TESTS and NPTESTS does not use Lilliefors correction prior to SPSS Statistics 21.0.0.1. Retrieved Nov 18 2016 from here.
Lilliefors, H. W. (1967). On the Kolmogorov-Smirnov test for
normality with mean and variance unknown, Journal of the
American Statistical Association, 62, 399–402.