1. What is Kurtosis?
- A positive value tells you that you have heavy-tails (i.e. a lot of data in your tails).
- A negative value means that you have light-tails (i.e. little data in your tails).
If you have a kurtosis close to 3, your data is considered nearly normal, with the tails slightly lighter or heavier than in an ideal standard distribution. This type of graph is known as ‘mesokutric’, and gives us insight into how much deviation from normality exists in our datasets.
Kurtosis is the fourth moment in statistics.
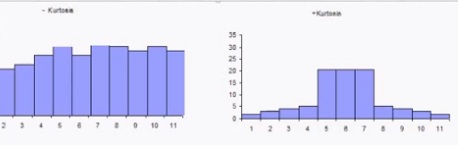
What is Excess kurtosis?
Excess kurtosis is a way to measure the deviation of tails in any given probability distribution from that of a normal distribution. Generally, if it’s zero or negative, there will be lighter tails than what one would expect in an ideal bell-shaped curve; on the other hand, heavier tails are expected when excess kurtosis is positive.
The following graph shows a variety of distributions. Note how the tails are fatter or thinner than the normal (black):
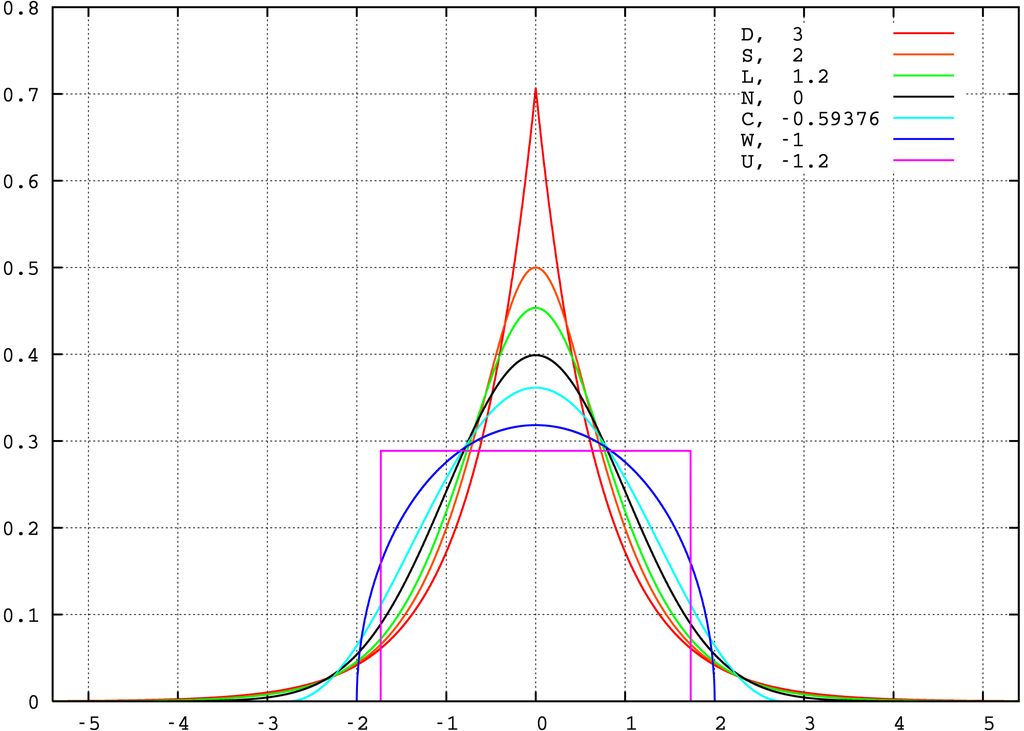
Key:
Red, kurt 3, Laplace (D)ouble exponential distribution;
Orange, kurt 2, hyperbolic (S)ecant distribution;
Green, kurt 1.2, (L)ogistic distribution;
Black, kurt 0, (N)ormal distribution;
Cyan, kurt −0.593762…, raised (C)osine distribution;
Blue, kurt −1, (W)igner semicircle distribution;
Magenta, kurt −1.2, (U)niform distribution.
Back to Top
Calculating Kurtosis.
Although kurtosis is a powerful statistical measure, there’s been no established consensus on the exact formula to use for its calculation. This means that which equation you opt for can be determined by your field of research, the software program in hand or even simply personal preference. Therefore it pays off to stay informed and know exactly what definition/equation is being utilized beforehand.
For Minitab and SPSS, you can find the option in the “Descriptive Statistics” tab.
Kurtosis in Excel 2013
Note: The “KURT” reported by Excel is actually the excess kurtosis. See the note on formulas above.
Watch the video or read the steps below:
There are two options in Excel for finding kurtosis: the KURT Function and the Data Analysis Toolpak (How to load the Data Analysis Toolpak).
Kurtosis Excel 2013: KURT function
Step 1: Type your data into columns in an Excel worksheet.
Step 2: Click a blank cell.
Step 3: Type “=KURT(A1:A99)” where A1:99 is the cell locations for your data.
Kurtosis Excel 2013: Data Analysis
Step 1: Click the “Data” tab and then click “Data Analysis.”
Step 2: Click “Descriptive Statistics” and then click “OK.”
Step 3: Click the Input Range box and then type the location for your data. For example, if you typed your data into cells A1 to A10, type “A1:A10” into that box
Step 4: Click the radio button for Rows or Columns, depending on how your data is laid out.
Step 5: Click the “Labels in first row” box if your data has column headers.
Step 6: Click the “Descriptive Statistics” check box.
Step 7: Select a location for your output. For example, click the “New Worksheet” radio button.
Step 8: Click “OK.”
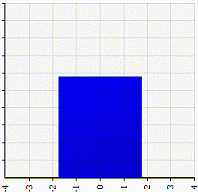
Platykurtic
Platykurtic distributions have negative kurtosis. The tails are very thin compared to the normal distribution, or — as in the case of the uniform distribution— non-existent.

An example of a very platykurtic distribution is the uniform distribution.
Leptokurtic
A leptokurtic distribution has excess positive kurtosis, where the kurtosis is greater than 3. The tails are fatter than the normal distribution. The following illustration1 shows a leptokurtic distribution along with a normal distribution (dotted line).
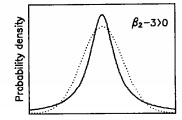
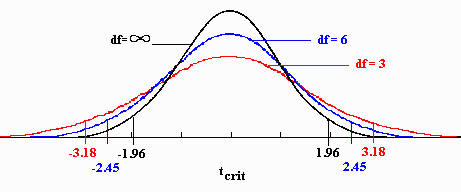
The Leptokurtic T-Test
The T distribution is an example of a leptokurtic distribution. It has fatter tails than the normal (you can also look at the first image above to see the fatter tails). Therefore, the critical values in a Student’s t-test will be larger than the critical values from a z-test.
Financial Markets
If you’re looking for a high risk/high reward investment, kurtosis may be your answer. Fund managers typically examine risks and returns when it comes to investments, taking into account whether something is lepto- or platy-kurtic; in other words if the return includes extreme outliers events that can cause more dramatic swings in value. For instance real estate (with a Kurt of 8.75) and High Yield US bonds (8.63), constitute higher risk investments while Investment grade US Bonds (1.06) and Small cap stocks 1(0).08 are deemed safer options – thus offering lower potential rewards but less volatility as well
References
Aldrich, E. (2014). Moments. Retrieved December 9, 2017 from: https://people.ucsc.edu/~ealdrich/Teaching/Econ114/LectureNotes/moments.html
DeCarlo, L. 1997. On the Meaning and Use of Kurtosis Psychological Methods. Vol 2. No.3, 292-307.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.
Wuensch, K. Undated. Skewness, Kurtosis, and the Normal Curve.
Check out our YouTube channel for more stats help and tips!