Krippendorff’s alpha (also called Krippendorff’s Coefficient) is an alternative to Cohen’s Kappa for determining inter-rater reliability.
Krippendorff’s alpha:
- Ignores missing data entirely.
- Can handle various sample sizes, categories, and numbers of raters.
- Applies to any measurement level (i.e. (nominal, ordinal, interval, ratio).
Commonly used in content analysis to quantify the extent of agreement between raters, it differs from most other measures of inter-rater reliability because it calculates disagreement (as opposed to agreement). This is one reason why the statistic is arguably more reliable, but some researchers report that in practice, the results from both alpha and kappa are similar (Dooley).
Computation of Krippendorff’s Alpha
The basic formula for alpha is a ratio (observed disagreement/expected disagreement). The ratio is deceptively simple, because the method is actually computationally complex, involving resampling methods like the bootstrap. This is a major disadvantage (Osborne). You can get an idea of the computations involved from the following formula.
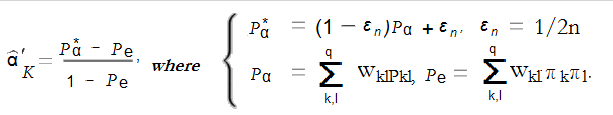
You can find a good example of just how complex the calculation can get in Krippendorf’s 2011 paper, Computing Krippendorff ‘s Alpha-Reliability (downloadable pdf). The Wikipedia entry also has a (somewhat esoteric) example, where construction of a coincidence matrix is outlined for a 3 rater, 15 item matrix.
Many macros to calculate alpha have been created, which opens up the use of Krippendorff’s alpha to a wider audience. These include:
- MATLAB: Various macros exist including Jana Eggink’s (downloadable here) and Jeffrey Girard’s (downloadable here).
What do the Results Mean?
Values range from 0 to 1, where 0 is perfect disagreement and 1 is perfect agreement. Krippendorff suggests: “[I]t is customary to require α ≥ .800. Where tentative conclusions are still acceptable, α ≥ .667 is the lowest conceivable limit (2004, p. 241).”
References:
Dooley, K. (2017).Questionnaire Programming Language. Interrater Reliability Report. Retrieved July 5, 2017 from: http://qpl.gao.gov/ca050404.htm.
Hayes, A.F. My Macros and Code for SPSS and SAS. Retrieved July 6, 2017 from: http://afhayes.com/spss-sas-and-mplus-macros-and-code.html
Hayes, A. F. & Krippendorff, K. (2007). Answering the call for a standard reliability measure for coding
data. Communication Methods and Measures 1,1:77-89.
Jason Osborne. Best Practices in Quantitative Methods.
Krippendorff, K. (2004). Content analysis: An introduction to its methodology. Thousand Oaks, California: Sage.
Krippendorff, K. (2011). “Computing Krippendorff’s alpha-reliability.” Philadelphia: Annenberg School for Communication Departmental Papers. Retrieved July 6, 2011 from: http://repository.upenn.edu/cgi/viewcontent.cgi?article=1043&context=asc_papers