Jeffrey’s prior (also called Jeffreys-Rule Prior), named after English mathematician Sir Harold Jeffreys, is used in Bayesian parameter estimation. It is an uninformative prior, which means that it gives you vague information about probabilities. It’s usually used when you don’t have a suitable prior distribution available. However, you could choose to use an uninformative prior if you don’t want it to affect your results too much.
The uninformative prior isn’t really “uninformative,” because any probability distribution will have some information. However, it will have little impact on the posterior distribution because it makes minimal assumptions about the model.
Jeffrey’s Prior Definition
Jeffreys prior is defined in terms of Fisher information, which tells us how much information about an unknown parameter we can get from a sample. In other words, Fisher Information tells us how well we can measure a parameter, given a certain amount of data. The formula for Jeffreys prior is:
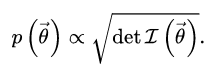
Where:
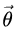 = a parameter vector.
= a parameter vector.- det I = determinant of the Fisher information matrix.
Jeffreys prior is especially useful because it is invariant under reparameterization of the given parameter vector.
Is it “Prior” or “Rule-Prior”?
Jeffreys didn’t always stick to using the Jeffreys rule prior he derived. For example, for the Poisson mean λ, he recommended
p(λ) α 1/λ,
instead of Jeffreys-rule prior
p(λ) α 1/√λ
despite the fact that the recommended formula doesn’t work when x = 0.
This can lead to a some confusion, because the priors he recommended in some cases (referred to sometimes as “Jeffreys Priors”) are not the same formulas as the one defined in the first section of this article. Some authors (like Li) suggest reserving the name “Jeffreys Priors” for Jeffreys recommendations, and using the (“correct”) term “Jeffreys-rule prior” for the formula he defined using Fisher information. This may be true, but the use of the term “Jeffreys Prior” is now so widespread that it’s too late to put the reins on the horse—which may mean it’s somewhat difficult to ascertain whether the formula you’re reading about in a text is “the” prior or just a recommendation.
References
Jeffreys, H. (1946). “An Invariant Form for the Prior Probability in Estimation Problems“. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 186 (1007): 453–461
Jeffreys, H. (1939). Theory of Probability. Oxford University Press.
Li, Y. (n.d.). The Jeffreys Prior. Retrieved February 8, 2018 from: http://ybli.people.clemson.edu/f14math9810_lec6.pdf