Statistics Definitions > Inverse Normal Distribution
What is an Inverse Normal Distribution?
An inverse normal distribution is a way to work backwards from a known probability to find an x-value. It is an informal term and doesn’t refer to a particular probability distribution.
Note: the Inverse Gaussian Distribution and Inverse Normal Distribution are often confused. See this comment at the end of the article for clarification.
How to Find Inverse Normal on the TI-83 with the InvNorm Command
The InvNorm function (Inverse Normal Probability Distribution Function) on the TI-83 gives you an x-value if you input the area (probability region) to the left of the x-value. The area must be between 0 and 1. You must also input the mean and standard deviation.
Sample question: Find the 90th percentile for a normal distribution with a mean of 70 and a standard deviation of 4.5.
Step 1: Press 2nd then VARS to access the DISTR menu.
Step 2: Arrow down to 3:invNorm( and press ENTER.
Step 3: Type the area, mean and standard deviation in the following format:
invNorm (probability,mean,standard deviation).
For this example, your input will look like this:
invNorm(90,70,4,.5).
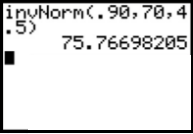
The x-value (90th percentile) is 75.767.
What is the Difference Between Inverse Normal Distribution and Inverse Gaussian Distribution?
The names “Gaussian Distribution” and “Normal Distribution” mean the same thing (i.e. a bell shaped curve). Physicists use the term Gaussian and Statisticians use the term “Normal.” However, The inverse normal distribution is not the same thing as the Inverse Gaussian distribution. The inverse normal distribution refers to the technique of working backwards to find x-values. In other words, you’re finding the inverse. The inverse Gaussian is a two-parameter family of continuous probability distributions. The “inverse” in “inverse Gaussian” is misleading because the distribution isn’t actually an inverse. In fact, at large values of it’s shape parameter, the inverse Gaussian looks exactly like the normal distribution.