In a general sense, infinitely divisible means that any section of time and space can be divided into an infinite number of smaller and smaller pieces. For example, 10 feet can be subdivided into 1 foot sections, 0.1 foot sections, 0.00001 foot sections…and so on. However, infinite divisibility in probability theory has a more defined meaning. Specifically:
A probability distribution is infinitely divisible if it can be written as the sum of n independent and identically distributed random variables for any positive integer n.
Infinite divisibility is an important property of stable probability distributions. They are often seen in practical use such as waiting time theory and modeling problems as well as theoretical applications like limit theorems.
Defining Infinite Divisibility
If the probability distribution F is infinitely divisible, then for any positive integer n, there is a variable Sn which can be written as
Sn = Xn1 + Xn2 + …. + Xnn
such that each of the Xn are random variables, independent and identically distributed; their sum, Sn, has the probability distribution F.
Infinite Divisibility and Characteristic Functions
One of the easiest ways of figuring out if a function is infinitely divisible is looking at its characteristic function. That’s because, if Φ(ω) is a characteristic function of your distribution F and Φn(ω) is the characteristic function of each of your independent identically distributed variables, then:
Φ(ω) = [Φn(ω)]n.
(Remember, they all have identical probability distributions, so their characteristic function is the same.)
So we can derive the characteristic function of our summed random variables from our original probability function by looking at the inverse of that,
Φn(ω) = [Φ(ω)]1/n.
This useful formula allows us to test whether or not a probability distribution is infinitely divisible. Our first step can be to calculate the hypothetical characteristic function of the summands, if they exist.
Examples of Infinitely Divisible Probability Distributions
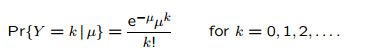
The Poisson distribution is an infinitely divisible distribution.
For each μ >0, and each n∈ {1, 2, 3,…}, independent random variables Xn1, Xn2,…Xnn have a Poisson distribution.
The normal distribution, the chi-squared distribution and the Cauchy distribution are also examples of infinitely divisible distributions. In fact, every stable distribution is infinitely divisible. However, the reverse isn’t true— not every infinitely divisible distribution is stable.
The binomial distribution and the uniform distribution are not infinitely divisible; the same is true of any distribution that is bounded — restricted to a certain range (Sato, 1999).
References
Sato, Ken-iti (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press. p. 31.
Sheffield, S. (2014) Infinite divisibility and Lévy processes. Article posted on website MIT.edu. Retrieved November 24, 2017 from: https://ocw.mit.edu/courses/mathematics/18-175-theory-of-probability-spring-2014/lecture-slides/MIT18_175S14_Lecture20.pdf
Watkins, T. (n.d.) Infinitely Divisible Random Variables and Their Characteristic Functions, Article posted on the San Jose University website. Retrieved November 24, 2017 from: http://www.sjsu.edu/faculty/watkins/infdiv.htm