Probability > How to Use a Probability Tree
Probability trees are useful for calculating combined probabilities for sequences of events. It helps you to map out the probabilities of many possibilities graphically, without the use of complicated probability formulas.
Watch the video for an example.
Why Use a probability tree?
Sometimes you don’t know whether to multiply or add probabilities. A probability tree makes it easier to figure out when to add and when to multiply. Plus, seeing a graph of your problem, as opposed to a bunch of equations and numbers on a sheet of paper, can help you see the problem more clearly.
Parts of a Probability Tree Diagram
A probability tree has two main parts: the branches and the ends(sometimes called leaves). The probability of each branch is generally written on the branches, while the outcome is written on the ends of the branches.
Multiplication and Addition
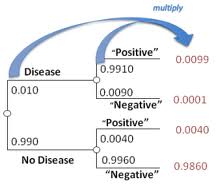
Probability Trees make the question of whether to multiply or add probabilities simple: multiply along the branches and add probabilities down the columns. In the following example (from Yale University), you can see how adding the far right column adds up to 1, which is what we would expect the sum total of all probabilities to be:
.9860 + 0.0040 + 0.0001 + 0.0099 = 1
Real Life Uses
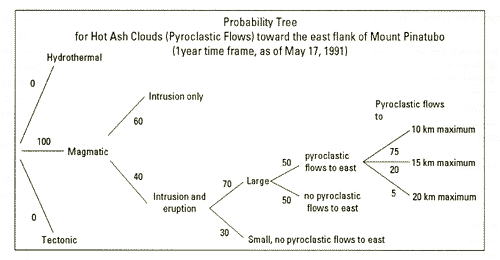
Probability trees aren’t just a theoretical tool used the in the classroom—they are used by scientists and statisticians in many branches of science, research and government. For example, the following tree was used by the Federal government as part of an early warning program to assess the risk of more eruptions on Mount Pinatubo, an active volcano in the Philippines.
How to Use a Probability Tree or Decision Tree
Sometimes, you’ll be faced with a probability question that just doesn’t have a simple solution. Drawing a probability tree (or tree diagram) is a way for you to visually see all of the possible choices, and to avoid making mathematical errors. This how to will show you the step-by-step process of using a decision tree.
How to Use a Probability Tree: Steps
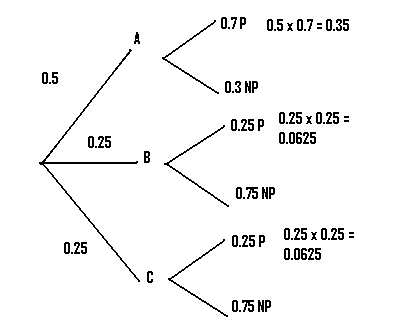
Example question: An airplane manufacturer has three factories A B and C which produce 50%, 25%, and 25%, respectively, of a particular airplane. Seventy percent of the airplanes produced in factory A are passenger airplanes, 25% of those produced in factory B are passenger airplanes, and 25% of the airplanes produced in factory C are passenger airplanes. If an airplane produced by the manufacturer is selected at random, calculate the probability the airplane will be a passenger plane.
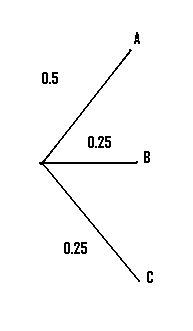
Step 1:Draw lines to represent the first set of options in the question (in our case, 3 factories). Label them: Our question lists A B and C so that’s what we’ll use here.
Step 2: Convert the percentages to decimals, and place those on the appropriate branch in the diagram. For our example, 50% = 0.5, and 25% = 0.25.
Step 3: Draw the next set of branches. In our case, we were told that 70% of factory A’s output was passenger. Converting to decimals, we have 0.7 P (“P” is just my own shorthand here for “Passenger”) and 0.3 NP (“NP” = “Not Passenger”).
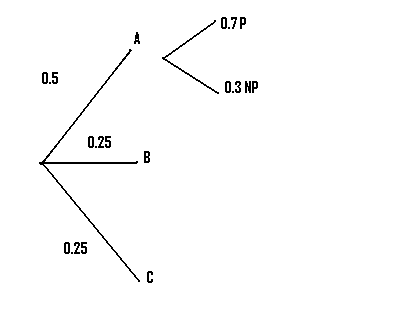
Step 4:Repeat step 3 for as many branches as you are given.
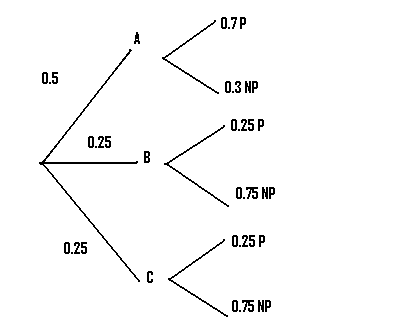
Step 5: Multiply the probabilities of the first branch that produces the desired result together. In our case, we want to know about the production of passenger planes, so we choose the first branch that leads to P.
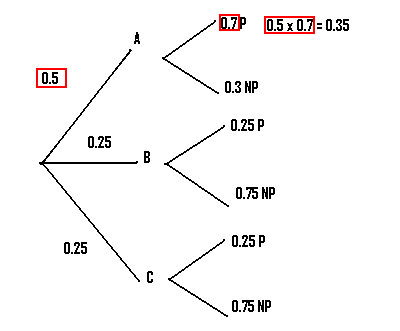
Step 6: Multiply the remaining branches that give the desired result. In our example there are two more branches that can lead to P.

Step 6: Add up all of the probabilities you calculated in steps 5 and 6. In our example, we had:
.35 + .0625 + .0625 = .475
That’s it!
Example 2
Example Question: If you toss a coin three times, what is the probability of getting 3 heads?
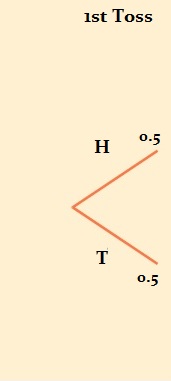
The first step is to figure out your probability of getting a heads by tossing the coin once. The probability is 0.5 (you have a 50% probability of tossing a heads and 50% probability of tossing a tails). Those probabilities are represented at the ends of each branch.
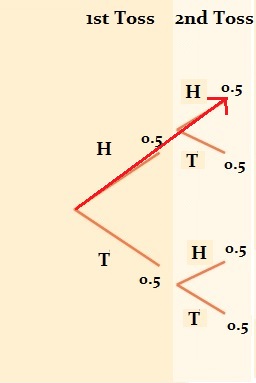
Next, add two more branches to each branch to represent the second coin toss. The probability of getting two heads is shown by the red arrow. To get the probability, multiply the branches:
0.5 * 0.5 = 0.25 (25%).
This makes sense because your possible results for one head and one tails is HH, HT, TT, or TH (each combination has a 25% probability).
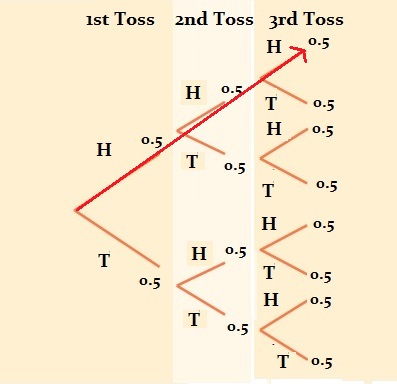
Finally, add a third row (because we were trying to find the probability of throwing 3 heads). Multiplying across the branches for HHH we get:
0.5 * 0.5 * 0.5 = 0.125, or 12.5%.
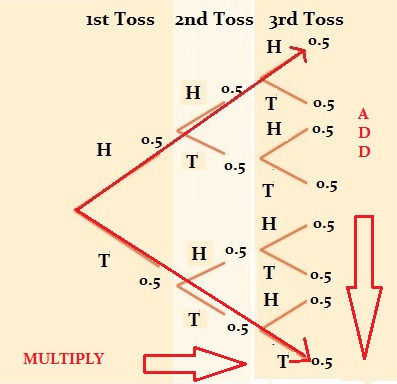
In most cases, you will multiply across the branches to get probabilities. However, you may also want to add vertically to get probabilities. For example, if we wanted to find out our probability of getting HHH OR TTT, we would first calculated the probabilities for each (0.125) and then we would add both those probabilities: 0.125 + 0.125 = 0.250.
Tip: You can check you drew the tree correctly by adding vertically: all the probabilities vertically should add up to 1.
Next: Tree Diagram Real Life Example
References
Punongbayan, R. et al. USGS Repository: Eruption Hazard Assessments and Warnings.