Statistics Definitions > Homogeneity & Homogeneous Data
What is Homogeneity?
A data set is homogeneous if it is made up of things (i.e. people, cells or traits) that are similar to each other. For example a data set made up of 20-year-old college students enrolled in Physics 101 is a homogeneous sample.
What is Homogeneous Sampling?
In homogeneous sampling, all the items in the sample are chosen because they have similar or identical traits. For example, people in a homogeneous sample might share the same age, location or employment. The selected traits are ones that are useful to a researcher. It is a type of purposive sampling and is the opposite of maximum variation sampling.
Homogeneous samples tend to be:
- Small.
- Made up of similar cases.
The opposite of a homogeneous sample is a heterogeneous sample. For this example, you might have a heterogeneous sample of 18-21 year old students in history 112, chemistry 211 and physics 101. The same is true for a heterogeneous population (all items in the population have different characteristics) and a homogeneous population (all items in the population have the same characteristics).
Homogeneous in More General Terms
In data analysis, a set of data is also considered homogeneous if the variables are one type (i.e. binary or categorical); if the variables are mixed (i.e. binary + categorical), then the data set is heterogeneous.
While it’s common in statistics to use “homogeneous” to mean the general sense of being the same, a data set can be analyzed mathematically to see if the data set is homogeneous. There are several ways to achieve this:
- Compare boxplots of the data sets.
- Compare descriptive statistics (especially the variance, standard deviation and interquartile range.
- Run a statistical test for homogeneity.
Statistical Tests
Running statistical tests for homogeneity becomes important when performing any kind of data analysis, as many hypothesis tests run on the assumption that the data has some type of homogeneity. For example, an ANOVA test assumes that the variances of different populations are equal (i.e. homogeneous).
One example of a test is the Chi-Square Test for Homogeneity. This tests to see if two populations come from the same unknown distribution (if they do, then they are homogeneous). The test is run the same way as the standard chi-square test; the Χ2 statistic is computed, and the null hypothesis (that the data comes from the same distribution) is either accepted or rejected.
Homogeneity of Variance
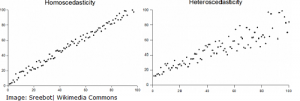
Homogeneity of variance (also called homoscedasticity) is used to describe a set of data that has the same variance. Visually, the data will have the same scatter on a scatter plot. If data does not have the same variance, it will show a heteroscedastic (“not the same”) scatter pattern.