Gumbel Distribution: Definition, Examples

Extreme Value Distributions > Gumbel Distribution

What is the Gumbel Distribution?

The Gumbel distribution (also called the Gumbel type) is a popular, asymmetric, extreme value distribution(EVD), used to model maximums and minimums. For example, the EVD Type I has been used to predict earthquakes, floods and other natural disasters, as well as modeling operational risk in risk management and the life of products that quickly wear out after a certain age. This skewed left distribution is also known as EVD type I.

There are two forms of EVD Type I: the minimum and maximum distributions.

1. Minimum Gumbel Distribution

The general form of the PDF for the minimum Gumbel is:

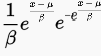
Where:

μ = the location parameter.
β = the scale parameter.

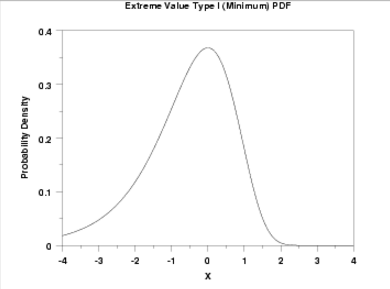
The probability density function has only one, unchanging shape which shifts according to the location parameter, μ. As μ increases, the distribution shifts to the left; As μ decreases, it shifts to the right.

When μ = 0 and β = 1, the distribution is called the Standard Gumbel Distribution (minimum). The PDF becomes:
e^x e^{-e^x}.

2. Maximum Gumbel Distribution

The general form of the PDF for the maximum Gumbel is almost the same (note the change in sign for the first exponent). The change in sign means that the shape of the PDF is an identical mirror image of the minimum Gumbel:

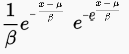
Making the PDF for the maximum standard Gumbel distribution:
e^-x e^{-e^x}.

The Gumbel distribution is also called the log-Weibull distribution and the double exponential, although the term “double exponential” is also used as another name for the Laplace distribution.

References

Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gumbel, E.J. (1954). Statistical theory of extreme values and some practical applications. Applied Mathematics Series 33 (1st ed.). U.S. Department of Commerce, National Bureau of Standards. ASIN
Gumbel, E. J. “Multivariate Extremal Distributions.” Bull. Inst. Internat. Statistique 37, 471-475, 1960a.
Gumbel, E. J. “Bivariate Logistic Distributions.” J. Amer. Stat. Assoc. 56, 335-349, 1961.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.