Graph Theory: Definitions for Common Terms

Statistics Definitions >

Graph Theory is the study of lines and points.

It is a sub-field of mathematics which deals with graphs: diagrams that involve points and lines and which often pictorially represent mathematical truths. Graph theory is the study of the relationship between edges and vertices. Formally, a graph is a pair (V, E), where V is a finite set of vertices and E a finite set of edges.

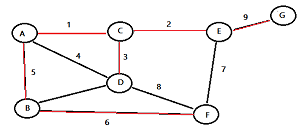
Definitions in Graph Theory

Graph Theory has some unique vocabulary:

• An arc is a directed line (a pair of ordered vertices).
• An edge is line joining a pair of nodes.
  • Incident edges are edges which share a vertex. A edge and vertex are incident if the edge connects the vertex to another.
• A loop is an edge or arc that joins a vertex to itself.
• A vertex, sometimes called a node, is a point or circle. It is the fundamental unit from which graphs are made.
  • Adjacent vertices are vertices which are connected by an edge.
  • The degree of a vertex is simply the number of edges that connect to that vertex. Loops count twice.
  • A predecessor is the node (vertex) before a given vertex on a path.
  • A successor is the node (vertex) following a given vertex on a path.
• A walk is a series of vertices and edges.
  • A circuit is a closed walk with every edge distinct.
  • A closed walk is a walk from a vertex back to itself; a series of vertices and edges which begins and ends at the same place.
  • A cycle is a closed walk with no repeated vertices (except that the first and last vertices are the same).
  • A path is a walk where no repeated vertices. A u-v path is a path beginning at u and ending at v.
  • A u-v walk would be a walk beginning at u and ending at v.

More Definitions:

• An edge contraction involves removing an edge from a graph by merging the two vertices it used to join.
• In computer science and computer-based graph theory, a graph traversal is an exploration of a graph in which the vertices are visited or updated one by one.
• A Hamiltonian cycle is a closed loop where every node is visited exactly once.

Types of Graphs

• An acyclic directed graph is a finite directed graph which has no directed cycles.
• A directed graph is a graph where the edges have direction; that is, they are ordered pairs of vertices.
• A condensation of a multigraph is the graph that results when you delete any multiple edges, leaving just one edge between any two points.
• If a graph has a path between every pair of vertices (there is no vertex not connected with an edge), the graph is called a connected graph.
• If a graph G’ can be constructed from a graph G by repeated edge contractions or deletions, the graph G’ is a graph minor of G.
• An inverted graph G’ of G is a graph with the same vertices but none of the same edges; two vertices in G’ are adjacent if and only if they were not adjacent in G.
• A multigraph is a graph without loops, but which may have multiple edges.
• A null graph is a graph with no edges. It may have one or more vertices.
• An oriented graph is a directed graph that doesn’t have any symmetric pairs of directed edges.
• A simple graph is a graph that doesn’t have any loops or multiple edges. No multiple edges means that no two edges have the same endpoints.
• A subgraph is a graph whose vertices and edges are included in the vertices and edges of another graph (the supergraph).
• A symmetric graph is a directed graph D where, for every arc (x,y), the inverted arc (y,x) is also in D.
• A trivial graph is a graph with only one vertex.
• An undirected graph is a graph where none of the edges have direction; the pairs of vertices that make up each edge are unordered.

Graph Theory in History

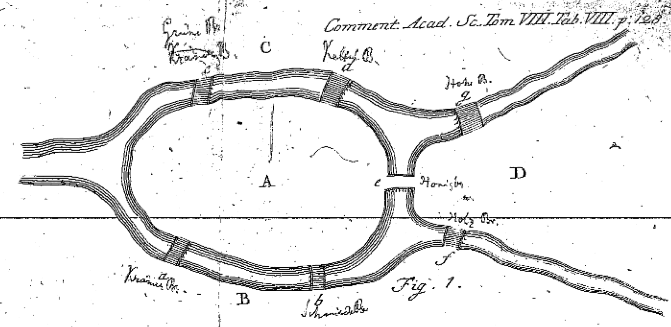
Graph Theory dates back to 1735 and Euler’s Seven Bridges of Königsberg. The city of Königsberg was a town with two islands, connected to each other and to the mainland by seven bridges. The question set was whether it were possible to take a walk and cross each bridge exactly once. In a first demonstration of graph theory, Euler showed that it was not possible.

Mantel’s Theorem

Mantel’s theorem, published in 1907, tells us the largest number of edges a graph with a given number of vertices may have without having a triangle for a subgraph. It can be stated as:

A graph with n vertices and m edges will contain a triangle as a subgraph if and only if m > n²/4.

Related Articles

Binary Trees.
The Traveling Salesman Problem.

References

Introduction to Combinatorics and Graph Theory. Retrieved 8/11/2017 from: https://www.whitman.edu/mathematics/cgt_online/cgt.pdf
Turan’s Theorem
Mathematics of Bioinformatics