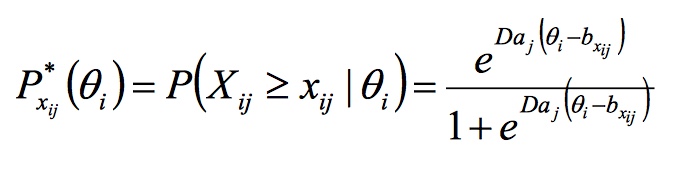Graded Response Model / Ordered Categorical Responses Model

What is a Graded Response Model?

Graded response model (or Ordered Categorical Responses Model) is a family of mathematical models for grading responses. Specifically, responses with ordered polytomous categories.

Ordered means that there is a specific order, or ranking, of responses.
Polytomous means that these response are divided into more than two secondary parts or branches, as opposed to dichotomous responses (i.e. responses with two categories).

Therefore, graded response models are used to model assessments where the scores are given in more detail than simply a binary ‘correct/incorrect’. These models includes things as:

Letter grades (A, B, C, D, E),
Responses to pain, graded on a 1 to 10 scale,
“Strongly disagree, disagree, neutral, agree, strongly agree’ in the response to a survey question.

Purpose of the Graded Response Model

The graded response model has three main purposes.

It allows us to evaluate, or at least estimate, the probability a particular test subject will receive a specific grade or score for each item
It allows us to estimate the test subject’s level of ability or latent trait.
It allows us to estimate how well the test questions measure that latent trait or ability.

Calculating Probability in the Graded Response Model

The graded response model can be summarized by the equation

P(X_ij = x _ij | θ _i) = P^*_{x_ij}(θ_i) – P^*_{x_ij+1} ( θ_i )

Where:

θ represents the latent ability or trait, and its actual level in the test subject.
x_ij represents the grade given.
b_jx is a constant specific to the test item; the location parameter, or category boundary for score x; the point on the ability scale where P = 0.5.
a_jx is an another constant specific to the test item, the discrimination parameter, and is constant over response categories for a given item.
D is a scale factor.

References

Matteucci, Mariagiulia & Stracqualursi, Luisa. (2006). Student assessment via graded response model. Statistica. 66. 435-447. 10.6092/issn.1973-2201/1216. Retrieved from https://www.researchgate.net/publication/227377692_Student_assessment_via_graded_response_model on April 21, 2018
Samejima, Fumiko. Handbook of Modern Item Response Theory, ch. 6 (pp.85-100). Retrieved from https://www.researchgate.net/publication/279369018_Graded_Response_Model on April 21, 2018.
SAS Support, Graded Response Models.
Retrieved from https://support.sas.com/rnd/app/stat/examples/graded/graded.pdf on April 21, 2018.
Templin, Jonathan. IRT Models for Polytomous Response Data. American Board of Internal Medicine Item Response Theory Course. Retrieved from https://jonathantemplin.com/files/irt/irt07abim/irt07abim_lecture03.pdf on April 21, 2018