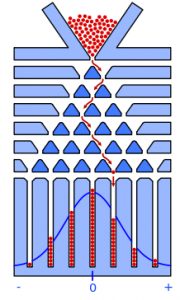
The Galton board (also called a Quincunx) is a physical model of the binomial distribution which beautifully illustrates the central limit theorem; When you add independent random variables, their sum tends toward a normal distribution. In particular, it demonstrates that the binomial distribution is approximately a normal distribution.
Invented by Sir Francis Galton (1822-1911), the Galton board is a vertically placed rectangular board with evenly spaced pegs or nails (represented by triangles in the image) over its upper half. A funnel with a slot just large enough to let out one ball at a time is placed near the top. In the lower half of the board are rectangular slots, each just as wide as the balls that will be used for the experiment. The funnel is placed so that a ball which comes through it will hit one of the first row of nails squarely in the center.
Typically, a glass cover is put over the whole setup so to watch the progress of balls through the funnel.
Where to Find Galton Boards
I own this excellent Galton board from Four Pines publishing.
It’s one of the more inexpensive Galton Board’s on the market, but it’s well made and comes packaged in a classy, professional box. As well as being a somewhat addictive desktop gadget, it demonstrates other concepts as well, including Pascal’s Triangle and regression to the mean.
I highly recommend this product for your classroom, your desk, or as a gift to your favorite mathematician. Get yours on Amazon and shipping is free!
Running a Galton Board Demonstration
To run an experiment demonstrating the shape of the binomial distribution, a large number of balls must be placed in the funnel and allowed to run into the peg-board below. Each ball, as it falls, will strike the nail under the funnel, and will bounce either left or right— So pl = 1- pr. In other words, the probability of a ball going left (pl) is 1 minus the probability of a ball going right (pr). If the pegs are symmetrically arranged, pl = pr = ½.
These balls will continue bouncing against the pegs below. At each peg the ball will randomly ‘choose’ one of two directions—left or right—to go around it. Eventually, each ball will fall into one of the slots at the bottom.
Each step is random, so if the ball hits n pegs on its downward journey, which slot the it finally ends up in can be considered as the sum of n random variables. As the central limit theorem tells us that the sum of k random variables approaches a normal distribution as k increases, we can expect that the distribution in our slots will be normal. We should see a large ‘bell’ or bump in the center of the board, tapering off at both edges. This distribution will grow closer and closer to normal the larger the number of pegs our board has, and the larger the number of balls that are dropped.
References
Starnes, D. (2009). Statistics Through Applications. Macmillan.
Quincunx Applet & the Central Limit Theorem. Retrieved from
http://www.stat.ucla.edu/~dinov/courses_students.dir/Applets.dir/QuincunxApplet.html on November 30, 2017