Statistics Definitions > Fisher’s Exact Test of Independence
What are nominal variables?
What is a contingency table?
In order to understand Fisher’s, you may want to read these articles first:
What is Fisher’s Exact Test of Independence?
Fisher’s Exact Test of Independence is a statistical test used when you have two nominal variables and want to find out if proportions for one nominal variable are different among values of the other nominal variable. For experiments with small numbers of participants (under around 1,000), Fisher’s is more accurate than the chi-square test or G-test.
Unlike other statistical tests, there isn’t a formula for Fisher’s. To get a result for this test, calculate the probability of getting the observed data using the null hypothesis that the proportions are the same for both sets.
Fisher’s Exact Test of Independence example situation:
You are studying if certain treatments for skin cancer lead to good outcomes. The first nominal variable is the treatment: some patients are given drug X and others are given drug Y. The second nominal variable is the outcome: patients are cured of cancer, or they are not. When you complete the study of 50 patients, you find that the percentage of patients who were cured and took drug X is much higher than patients who took drug Y. Fisher’s Exact Test of Independence will tell you if your results are statistically significant.
Calculation
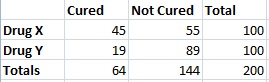
Fisher’s Exact Test of Independence uses a contingency table to display the different outcomes for an experiment. Although it’s possible to calculate it by hand (you can find the procedure here — scroll down to “Fisher Exact Probability Test: Logic and Procedure”), why would you want to? For more than a handful of entries, the calculations can be very tedious.
Note on one sided and two sided tests: the one-sided Fisher’s tests if a result is greater than or less than a certain amount. The two sided Fisher’s tests if a result is different from a certain proportion. In most cases, you’ll probably use a two-sided test.
You can find an online calculator for Fisher’s Exact test here. It’s also possible to calculate it in Microsoft Excel. Download this Excel worksheet and replace the entries with your data.