What is Dunn’s Test?
Once your initial ANOVA has found a significant difference in three or more means, Dunn’s Test can be used to pinpoint which specific means are significant from the others. Dunn’s Multiple Comparison Test is a post hoc (i.e. it’s run after an ANOVA) non parametric test (a “distribution free” test that doesn’t assume your data comes from a particular distribution).
It is one of the least powerful of the multiple comparisons tests and can be a very conservative test—especially for larger numbers of comparisons. For example, if you have 10 comparisons at an alpha level of .05 then the formula results in a very per-comparison error rate of .005.
- The null hypothesis for the test is that there is no difference between groups (groups can be equal or unequal in size).
- The alternate hypothesis for the test is that there is a difference between groups.
Dunn’s test divides the overall alpha level by the number of comparisons:
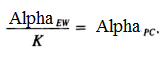
Dunn vs. Tukey and Dunnett
The Dunn is an alternative to the Tukey test when you only want to test for differences in a small subset of all possible pairs; For larger numbers of pairwise comparisons, use Tukey’s instead. Use Dunn’s when you choose to test a specific number of comparisons before you run the ANOVA and when you are not comparing to controls. If you are comparing to a control group, use the Dunnett test instead.
Dunn’s Test Table
If you’re calculating Dunn’s test by hand, you’ll need to reference a table of values that divides the 5% alpha level among the multiple comparisons. The table has a list of critical t values for odd Type I error probabilities. The use of Dunn’s table is somewhat archaic (most people would use software for the procedure), so you’ll have to reference an older text for the table, like Edwards (1985) or Dunn’s original text from 1961 (note: as of April 8, 2017 this link includes the full text and all tables). http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=6F118019A75299E92B1FC80EAAD8E642?doi=10.1.1.309.1277&rep=rep1&type=pdf
References:
Dunn, O.J. (1961) Multiple comparisons among means. JASA, 56: 54-64.
Edwards, A. (1984). An Introduction to Linear Regression and Correlation.