Differential equations have a derivative in them. For example, dy/dx = 9x. In elementary algebra, you usually find a single number as a solution to an equation, like x = 12. But with differential equations, the solutions are functions. In other words, you have to find an unknown function (or set of functions), rather than a number or set of numbers as you would normally find with an equation like f(x) = x2 + 9.
For example, the differential equation
dy⁄dx = 10x
is asking you to find the derivative of some unknown function y that is equal to 10x.
Differential equations represent the relationship between a varying quantity and it’s rate of change.
Contents:
- Autonomous Differential Equations
- Boundary Value Problems
- Order of a Differential Equation
- Kepler’s Laws & DiffEq
- Laguerre Differential Equations
- Linear Differential Equations
- Nonlinear Differential Equations
- Solving Ordinary Differential Equations
- Solution of Second Order Differential Equation.
What are Autonomous Differential Equations?
Autonomous differential equations have the form
y′ = f(y).
Although the independent variable doesn’t explicitly appear, these equations can also be written as
y′(x) = f(y(x)).
The right side of the equation is independent of x. As there aren’t any terms that depend on x, the equation is self-governing (which is another word for autonomous) [1]. To put that another way, the rate of change of x is only dependent on x itself; It isn’t dependent on time. All autonomous differential equations are characterized by this lack of dependence on the independent variable.
Many systems, like populations, can be modeled by autonomous differential equations. These systems grow and shrink independently—based only on their own behavior and not by any external factors. For example, a population of deer on an island with unlimited resources and no predators is autonomous. However, given a fluctuating number of predators, the system is no longer autonomous because the system now depends on an external factor— the predator population [2].
Properties of Autonomous Systems
All autonomous systems [3]:
- Model conditions which are constant in time.
- Are difficult to integrate but easy to solve (for the most part).
- Are separable. All autonomous equations can be solved (at least implicitly) by separating variables.
- Contain a wealth of qualitative information even if a solution can’t be found.
- Are time invariant (a horizontal shift of a solution is another solution). For example, if a solution is y(t) then y(t – t0) is also a solution.
Finding Solutions to Autonomous Differential Equations
Every critical point is a solution of the autonomous differential equation y′ = f(y). A critical point is a real number c so that f(c) = 0.
Complementary functions are one part of the solution to ADE’s.
Watch the following video which shows equilibrium solutions and stability of autonomous systems:
Autonomous Differential Equations: References
[1] Autonomous Differential Equations. Retrieved March 20, 2021 from: http://www.math.utah.edu/~gustafso/s2010/autonomousDE2008.pdf
[2] Nathan Pflueger (2011). Lecture 27: Autonomous equations. Retrieved March 20, 2021 from: https://npflueger.people.amherst.edu/math1b/Lecture27.pdf
[3] First Order Autonomous DEs’: Introduction. Retrieved March 20, 2021 from: https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/first-order-autonomous-differential-equations/MIT18_03SCF11_s10_0intro.pdf. CC 4.0.
Boundary Value Problems
A one-dimensional boundary value problem (BVP) is an ordinary differential equation, plus some boundary conditions (constraints) equal to the order of the differential equation (the order is the number of the highest derivative).
These problems are similar to initial value problems, which have conditions specified for the lowest end of the domain (the “initial” values). Boundary values are minimum or maximum values for some physical boundary.
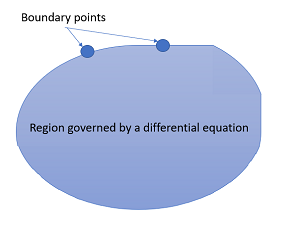
The conditions might involve solution values at two or more points, its derivatives, or both. For boundary value problems with some kind of physical relevance, conditions are usually imposed at two separate points. When solving boundary value problems, we are only interested in a solution between the two points.
Simple Example of a Boundary Value Problem
Example question: Find a function that satisfies the equation f′(x) = 2x for any x-values between 0 and 1. The function has a boundary value of 3 when x = 1.
Solution: Many functions can satisfy the equation f′(x) = 2x for any x-values between 0 and 1, but not all will meet the requirement for the stated boundary values (3, when x = 1).
For example, the function f(x) = x2 satisfies the differential equation, but it fails to satisfy the specified boundary values (as stated in the question, the function has a boundary value of 3 when x = 1). Plugging in x = 1, we get: f(1) = 12 = 1.
The function f(x) = x2 + 2 satisfies the differential equation and the given boundary values. The first derivative of f(x) = x2 + 2 = x2, and (plugging in the boundary values):
12 + 2 = 3.
Boundary Value Problem: References
Eriksson, K.; Estep, D.; Hansbo, P.; and Johnson, C. Computational Differential Equations. Lund: Studentlitteratur, 1996.
Powers, D. Boundary Value Problems: And Partial Differential Equations. Academic Press. (2006).
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. “Two Point Boundary Value Problems” and “Boundary Values Problems.” Ch. 17 and part of §19.0 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 753-787 and 829-833, 1992.
Order
The order of a differential equation refers to the highest derivative you can find in the function.
- First order differential equations (sometimes called ordinary differential equations) contain first derivatives and therefore only require one step to solve to obtain the function.
- Second order differential equations contain second derivatives.
The order of differential equations is equal to the order of the highest derivative in the equation.
How to Find the Order of Differential Equations
To determine the order of differential equations, follow these steps.
- Step 1: Identify the highest derivative in the differential equation.
- Step 2: If the highest derivative is of degree n, then the equation is an nth-order differential equation.
Example: Consider the differential equation below:
x5y + xy′ + 5y′′′ = 0
In this case, the highest order derivative is a third derivative. So, we call it a third-order differential equation.
Example: What is the order of the differential equation below?
d4y/dx4 + dy/dx = x
Here, the highest order derivative is a fourth derivative. Therefore, the differential equation is of fourth-order.
First-Order Differential Equations
One of the most common differential equations is a first-order differential equation. A differential equation of first order will have the following form:
a(x) * (dy/dx) + b(x) * y + c(x) = 0
One example of a real-world phenomenon you can model with a first-order differential equation is exponential growth. With this type of growth, a population’s change is directly proportional to its current size. In the equation below, N is the population size, t is time, k is the growth constant.
dN / dt – k * N = 0
Another example of a real-world first-order phenomenon is air resistance. Scientists can model the effects of air resistance as a drag force that is directly proportional to an object’s velocity. Below, m is the mass of the object, v is the object’s velocity, b is the fluid’s drag constant, and t is time:
m * (dv / dt) + b * v = 0
Second-Order Differential Equations
Another common differential equation that describes several natural phenomena is the second-order differential equation. These equations will have the following form:
a(x)*(d2y /dx2) + b(x) * (dy/dx) + c(x) * y + d(x) = 0
For example, Hooke’s Law states that the force on an object is directly proportional to the amount it is stretched. Hooke’s Law is modeled by the equation below:
m * (d2x / dt2) + k * x = 0
Where:
- m is the object’s mass,
- x is the object’s position,
- k is the spring constant, and
- t is time.
Second-order differential equations can also be found in several electronic circuits. For example, a special type of circuit called an “RLC” circuit is modeled by this differential equation:
L *(d2q / dt2) + R * (dq/dt) + (1/C) * q = 0
Where:
- L is inductance,
- R is resistance,
- C is capacitance,
- q is charge, and
- t is time.
Order in Partial Differential Equations
A partial differential equation is one with multiple partial derivatives. To assign the order of a partial differential equation, only consider the derivative of the highest order.
Example: The distribution of heat across a solid is modeled by the following partial differential equation (also known as the heat equation):
(∂w / ∂t) – (∂2w / ∂x2) = 0
Although the highest derivative with respect to t is 1, the highest derivative with respect to xis 2. Therefore, the heat equation is a second-order partial differential equation.
Order in Nonlinear Differential Equations
For a nonlinear differential equation, the same rules for determining order apply. This is true even if some terms in the equation are a product of several derivatives.
Example: What is the order of the nonlinear differential equation below?
y′y′ + xy′′ = 0
Since the highest order derivative is a second-order derivative, the differential equation is a second-order nonlinear differential equation.
In summary, finding the order of differential equations is a fairly straightforward process. Identify the highest order derivative in the equation, and classify the differential equation accordingly.
Kepler’s Laws and Differential Equations
Kepler’s Laws of planetary motion are:
- Planets revolve around the sun in an elliptical orbit; the sun is at one of the two foci.
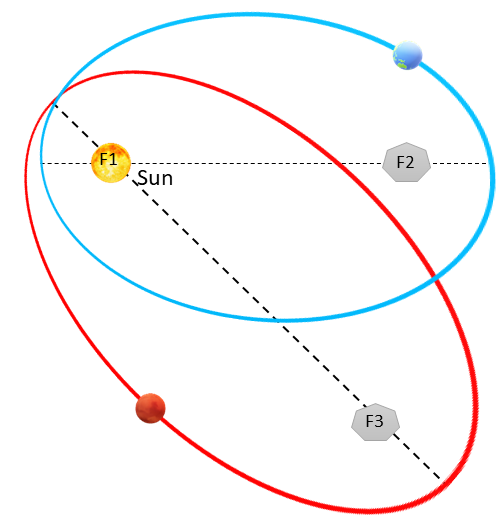
The foci are labeled F1 and F2 (blue planet) and F3 and F3 (red planet). - The line that joins the sun to a planet sweeps out equal areas in equal times.

Two months of the year are shaded in (labeled a1 and a2). Although they appear to be different in size, they have the same time period (one month, in this example), so they do have the exact same area. - A planet’s squared orbital period is directly proportional to the cube of the semi-major axis of its orbit. The third of Kepler’s laws allows us to compare the speed of any planet to another using a planet’s period (P)—the time it takes to go around the sun relative to the stars—and it’s average distance (d) from the sun. < /li>
All three of Kepler’s laws result from the following differential equation:
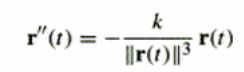
Where:
- r = r(t) is the vector from the sun to the planet
- m = planet’s mass
- || = magnitude or length of the vector
Laguerre Differential Equations
The Laguerre differential equation (sometimes just called the Laguerre equation) has the format (Dettman, 1986):
Where λ is a real number (n or k are sometimes used as notation instead of λ).
This ordinary differential equation is usually only of interest when λ is an integer and the interval is x ≥ 0 (Tenenbaum & Pollard, 1985, p.624). It has multiple applications in the study of optics and harmonic oscillators in quantum mechanics; The wave function for the hydrogen atom is the Laguerre differential equation.
In standard form, the equation becomes (Konstantogiannis, 2018):
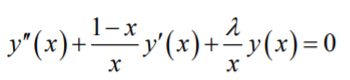
There is a regular singular point at x = 0 and an irregular singularity at ∞.
The equation and associated polynomials are named after Edmond Laguerre (1834-1866).
Laguerre Polynomials
The solutions to the Laguerre differential equation are the Laguerre polynomials (Glasgow, 2014). They can be expressed as a series (Joseph, 2019):
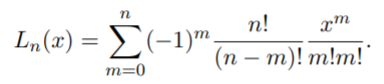
Or, alternatively by Rodrigue’s formula (Mahmoudi et al., 2012):
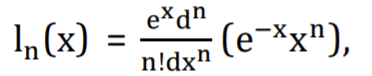
They can also be defined recursively by:
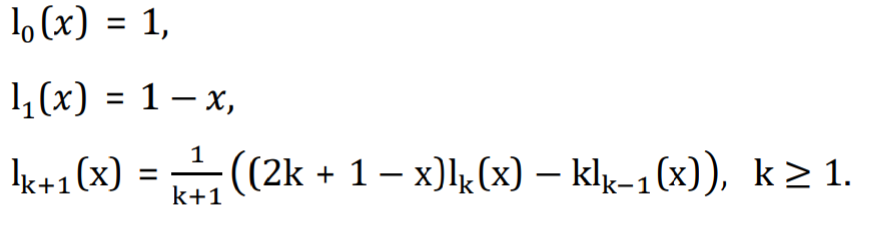
For example, the next few Laguerre polynomials are:
- l2 = ½ (x2 – 4x + 2),
- l3 = (1/6) (-x3 + 9x2 – 18x + 6).
- l4 = (1/24) (x4 – 16x3 + 72x2 – 96x + 24).
- l5 = (1/120) (-x5 + 25x4 – 200x3 + 600x2 – 600x + 120).
- l6 = (1/720) (x6 – 36x5 + 450x4 – 2400x3 + 5400x2 – 4320x + 720).
Laguerre Differential Equations: References
Dettman, J. (1986). Introduction to Linear Algebra and Differential Equations. Dover.
Glasgow, L. (2014). Applied Mathematics for Science and Engineering. Wiley.
Joseph, A. (2019). Phy310—Mathematical Methods for Physicists I. Retrieved August 25, 2020 from: https://web.iisermohali.ac.in/Faculty/anoshjoseph/courses/2019_odd_mmp1/lec12.pdf
Konstantogiannis, S. (2018). Polynomial and Non-Polynomial Terminating Series Solutions to the Associated Laguerre Differential Equation. Retrieved August 25, 20202 from: https://www.academia.edu/37908752/Polynomial_and_Non_Polynomial_Terminating_Series_Solutions_to_the_Associated_Laguerre_Differential_Equation
Mahmoudi, Y. et al. (2012). Adomian Decomposition Method with Laguerre Polynomials for Solving Ordinary Differential Equation. Retrieved August 25, 2020 from: https://www.textroad.com/pdf/JBASR/J.%20Basic.%20Appl.%20Sci.%20Res.,%202(12)12236-12241,%202012.pdf
Tenenbaum, M. & Pollard, H. (1985). Ordinary differential equations : an elementary textbook for students of mathematics, engineering, and the sciences. Dover Publications.
Linear Differential Equations
Linear differential equations are differential equations with the form
h(x) + f0(x)y + f1(x)y′ + f2(x)y′′ + … + fn(x)y(n) = 0
In this case, functions h and f0…fn are differentiable functions , and y is a polynomial of x.
Ordinary or Partial Linear Differential Equations
A linear differential equation can be either an ordinary differential equation or a partial differential equation.
- Linear ordinary differential equations have functions that depend on one variable,
- Linear partial differential equations have functions that depend on multiple variables.
Example: The wave equation is a differential equation that describes the motion of a wave across space and time. It can be written as follows:
∂2u / ∂t2 – c2* (∂2u / ∂x2) = 0
Since the wave equation is a linear differential equation, since it follows the general form described above. The function u, representing the height of the wave, is a function of both position, x, and time, t. So, the wave equation is a linear partial differential equation.
Example: The force of gravity near Earth’s surface can be modeled by the differential equation
d2r / dt2 + 9.8 = 0
This equation follows our model for linearity, where h(x) = 9.8, and f2(r) = 1. Additionally, the function r, representing the height of some object, is only a function of one variable: t. Therefore, the equation is a linear ordinary differential equation.
Homogenous vs. Non-Homogeneous Linear Differential Equations
Consider the general form of a linear differential equation below:
h(x) + f0(x)y + f1(x)y′ + f2(x)y′′ + … + fn(x)y(n) = 0
A homogeneous linear differential equation is one where h(x) = 0. Conversely, a non-homogeneous linear differential equation is one in which h(x) ≠ 0.
Homogeneous linear differential equations benefit from the principle of superposition. The principle of superposition states that if y1 and y2 are solutions of a homogeneous linear differential equation, then
y = c1*y1 + c2*y2
is also a solution, where c1 and c2 are arbitrary constants.
Example Problem: Hooke’s Law, the physical law that explains the forces governing a mechanical spring, obeys the following homogeneous linear differential equation:
m(d2x / dt2) + kx = 0
Given that x1=sin(t) and x2=cos(t) are solutions to Hooke’s Law, find a general solution.
Answer: Since x1 and x2 represent solutions, and the differential equation is linear and homogeneous, the principle of superposition applies. Therefore, the general solution to Hooke’s Law is:
x(t) = c1*sin(t) + c2*cos(t)
where c1 and c2 could be any constant.
Nonlinear Differential Equations
Most differential equations are not of the linear form. These are called nonlinear differential equations.
Example: The motion of a swinging pendulum is described by the following differential equation.
(d2θ / dt2) + (g / L) * sin(θ) = 0
In this case, the differential equation does not satisfy our condition for linearity, because sin(θ) is not a polynomial function of θ. Therefore, the differential equation is nonlinear.
There are many analytical strategies for solving a linear differential equation, such as separation of variables (commonly used to find a particular solution), or the principle of superposition (commonly used to find a general solution). Unfortunately, the methods for solving a nonlinear differential equation are few and far apart because many non-linear functions are exceedingly difficult to integrate. Therefore, most non linear differential equations are solved by approximation.
Solutions to Particular, General, and Initial Conditions
A differential equation comes in many different guises. How you solve them depends on if you need a general or particular solution, or if an initial value problem is specified.
General solutions are where the solution is a function or set of functions. For example, the differential equation dy⁄dx = 2x means that you have to find the derivative of some unknown function y that is equal to 10x. You’ll always need to add a constant (+ C) as these are general (as opposed to particular) solutions. See: How to Find the General Solution for a Differential Equation.
A particular solution requires you to find a solution that meets the specific constraints given in the question. For example, while
dy⁄dv x3 + 8
requires a general solution (with + C), the differential equation
dy⁄dv x3 + 8; f(0) = 2
requires a particular solution, one that fits the constraint f(0) = 2. See:
How to Find a Particular Solution for Differential Equations.
initial value problems are where you are given an initial condition (for example, the initial condition y(0) = 3); You must find a particular solution that satisfies the initial condition. For example, the differential equation
dy⁄dx 19 x2 + 10; y(10) = 5
requires you to find a particular solution (a single function) that satisfies y(10) = 5. See: How to Solve a Differential Equation with an Initial Condition
How to Solve an Ordinary Differential Equation.
Ordinary differential equations have a function as the solution rather than a number. An ordinary differential equation contains information about that function’s derivatives.
You may have to solve an equation with an initial condition or it may be without an initial condition. For example, the differential equation
ds⁄dt = cos(x)
is an ordinary differential equation, but
ds⁄dt = cos(x); y(π) = 0
is an ordinary differential equation with an initial condition, y(π) = 0.
You’ll find two procedures below: one for “with” and one for “without” initial conditions.
1. Solve ordinary differential equations without initial conditions
Example problem: Solve ds⁄dt = cos t + sin t
Step 1: Use algebra to make the equation integrable. “Integrable” just means that you want to get the equation into a form that allows you to use one of the rules of integration. For this particular question, you need to get ds on its own, so divide by dt to get:
- ds = cos t + sin t dt
Note: That particular form is one you can fairly easily integrate with an integration rule for trigonometric identities. The two rules that apply here:
- ∫ cos x dx = sin x + C
- ∫ sin x = -cos x + C
Step 2: Integrate both sides of the equation:
- ∫ds = ∫cos t + sin t dt →
- ∫1 ds = ∫cos t + sin t dt →
- s = sin t – cos t + C
That’s it!
2. Solve an ordinary differential equation with initial conditions
dy⁄dx 3x2 – 5x – 9; y(1) = 10.5
Step 1: Use algebra to make the equation integrable:
- dy = 3x2 – 5x + 9 dx
Step 2: Integrate both sides of the equation:
- ∫dy = ∫3x2 – 5x + 9 dx →
- ∫1 dy = ∫3x2 – 5x + 9 dx →
- y = 3x3 – 2.5x2 + 9x + C
Step 3: Insert the values from the initial condition into the equation:
- 10.5 = 3(13) – 2.5(1) + 9(1) + C
- 10.5 = 3 – 2.5 + 9 + C
- C = 1
The solution to the differential equation is y = 3x3 – 2.5x2 + 9x + 1
3. Euler’s Method
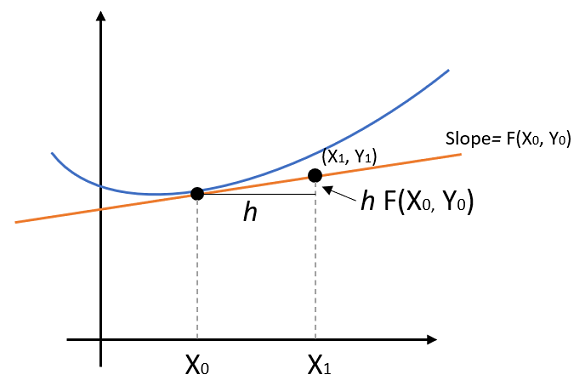
In other words, you could use it to solve a given first derivative and initial value:
dx/dy = F(x, y) and (x0, y0
The idea is that you use the initial value as a starting point to approximate the point you’re trying to get to. You take tiny steps, called a “step size” and crawl along the function. You’re literally taking steps (small changes in height and length) as you travel along the function. The step size Δh is typically 0.01 or less.
Example
Euler’s method is a little tedious, but this (relatively) short video gives a good example of the steps. Read below for a second example that uses a table to create a solution.
Example question: Use Euler’s method with a step value of 0.1 to find y(0.3) for the following initial value problem:
dy/dx = x + y, y(0) = 1
Step 1: Create a three column table. Put X as the first column header and Y as the second column header. The initial value is given in the question as y(0) = 1, so our starting point is:
X = 0
Y = 1
| X | Y | … |
| 0 | 1 | … |
Step 2: Add the step size (0.1) to the x-value in column 1. Continue to add that step size until you reach the requested x-value (given in the question as 0.3).
| X | Y | … |
| 0 | 1 | … |
| 0.1 | … | … |
| 0.2 | … | … |
| 0.3 | … | … |
Step 3: Use Euler’s formula dy/dx Δh + y to figure out the third column header.
You’re given dy/dx = x + y in the question, and your step size Δh is 0.1, so the formula for this particular question becomes:
dy/dx Δh + y =
(x + y) (0.1) + y
| X | Y | (x + y) (0.1) + y |
| 0 | 1 | … |
| 0.1 | … | … |
| 0.2 | … | … |
| 0.3 | … | … |
Step 4: Plug your values into the formula to get the first entry in column 3:
(0 + 1)(0.1) + 1
| X | Y | (x + y) (0.1) + y |
| 0 | 1 | (0 + 1)(0.1) + 1 |
| 0.1 | … | … |
| 0.2 | … | … |
| 0.3 | … | … |
Step 5: Solve the formula from Step 4 to get the y-value for the next entry in column 2:
(0 + 1)(0.1) + 1 = 1.1
| X | Y | (x + y) (0.1) + y |
| 0 | 1 | (0 + 1)(0.1) + 1 |
| 0.1 | 1.1 | … |
| 0.2 | … | … |
| 0.3 | … | … |
Step 6: Repeat Steps 4 and 5 using the new x and y values from the corresponding line in the table. Solve to get your next y-value:
(0.1 + 1.1)(0.1) + 1.1 = 1.22
| X | Y | (x + y) (0.1) + y |
| 0 | 1 | (0 + 1)(0.1) + 1 |
| 0.1 | 1.1 | (0.1 + 1.1)(0.1) + 1.1 |
| 0.2 | 1.22 | … |
| 0.3 | … | … |
Step 7: Repeat Step 6 for as many values as you need (until you get to your desired x-value, which is 0.3 in this example).
| X | Y | (x + y) (0.1) + y |
| 0 | 1 | (0 + 1)(0.1) + 1 |
| 0.1 | 1.1 | (0.1 + 1.1)(0.1) + 1.1 |
| 0.2 | 1.22 | (0.2 + 1.22)(0.1) + 1.22 |
| 0.3 | 1.362 |
The solution:
Y(0.3) = 1.362
Euler’s Method is Only an Approximation!
While the method is relatively simple to use, it’s a crude approximation for a solution so should be used with caution. For example, let’s say you wanted to approximate the value of y(1.5), given the initial value problem y′ = 2xy, y(1) = 1.
With a step size of 0.1, you should get the following values:
| yn | Actual value | Absolute Error | % Relative Error |
| 1.0000 | 1.0000 | 0.0000 | 0.00 |
| 1.2000 | 1.2337 | 0.0337 | 2.73 |
| 1.4640 | 1.5527 | 0.0887 | 5.71 |
| 1.8154 | 1.9937 | 0.1784 | 8.95 |
| 2.2874 | 2.6117 | 0.3244 | 12.42 |
| 2.9278 | 3.4903 | 0.5625 | 16.12 |
Note the large relative error (16%). This is in indication that you need to go with a smaller step size (a lot smaller!).
Another issue with Euler’s method is that it can only be used for well-behaved functions that don’t rapidly change over time. Often, you can’t tell that just by looking at the problem, although rapid changes should become obvious once you create table.
Laplace Transform
The Laplace transform is an integral transform— a way to solve certain ordinary differential equation problems via a type of integration. The method “magically simplifies” challenging problems [1], turning them from differential equations into algebraic ones, which makes them easier to solve.
The most important property of the Laplace transform is linearity, which means we can add a series of results together to solve a more complicated one.
Definition of Laplace Transform
The Laplace transform f(s) is defined as [2]:
![]()
Where:
- The integral ∫ is an indefinite integral.
- F(t) is the objective function.
- f(s) is called the image or resultant function.
The Laplace Transform of a function can usually be looked up in a table, without any need to integrate. A table of Laplace transforms can be found here.
How to Find a Laplace Transform
The general steps to find any Laplace transform:
- Look the function up in a table,
- If the function isn’t in a table, then integrate (using the formula).
- If the function isn’t integrable then break the function into component parts, then look those parts up in a table.
Example Problem #1: What is the Laplace Transform of the constant function f (t) = 1?
Step 1: Look up the function f(t) = 1 in the table. The function is at the top of page 2.
The Laplace transform is 1/s.
That’s it!
Example Problem #2: What is the Laplace Transform of f (t) = (3 + e6t)2?
Step 1: Look up the function f (t) = (3 + e6t)2 in the table.
This function is not in the table, so let’s move on to Step 2.
Step 2: Insert the function into the Laplace transform formula:
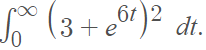
It’s also not easily integrable in its current form (I used Symbolab’s calculator to confirm this). So we need to move on to Step 3.
Step 3: Break the function into parts (we can do this because of the property of linearity). Expanding the expression, we get:
- f (t) = (3 + e6t)2
- = 9 + 6e6t + e12t.
Step 2: Look up the function parts in the table. We have three parts to look up in this example:
- 9
- 6 * e6t
- e12t
The solution is:
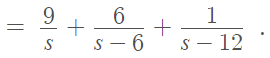
That’s it!
Laplace Transform: References
Boyd, S. Table of Laplace Transforms. Retrieved May 9, 2021 from: https://web.stanford.edu/~boyd/ee102/laplace-table.pdf
[1] The L.Transform. Retrieved May 9, 2021 from: https://lpsa.swarthmore.edu/LaplaceXform/FwdLaplace/LaplaceXform.html
[2] Dyke, P. (1999). An Introduction to LT’s and Fourier Series. Springer London.
Solution of Second Order Differential Equation.
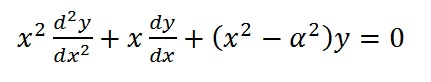
Second order differential equations contain second derivatives. Although they look a little intimidating at first, second order differential equations are solved in the exact same way as first order. They just require two steps to solve: one for the first derivative and one for the function itself.
Solution of Second Order Differential Equation: Steps:
Example Problem: Solve the following second order differential equation with the initial conditions:
- y′(0) = 4;
- y(1) = 5:
d2⁄dx2 = 2 – 6x
Step 1: Solve for y’ by integrating the differential equation:
y′ = ∫ (2 – 6x) dx →
y′ = 2x – 6x2⁄2 + C
Step 2: Plug the first initial value y′(0) into the equation from Step 1. y′(0) = 4, so when x = 0, y = 4:
4 = 2(0) – 3(0)2⁄2 + C →
c = 4
Therefore, y′ = 2x – 3x2 + 4
Step 3: Integrate the solution from Step 2 to get the function:
y = ∫2x – 3x2 + 4 →
y = x2 – x3 + 4x
Step 4: Plug the second initial value y(1) = 5 into the equation from Step 3.
5 = 12 – 13 + 4(1) + C
C = 1
Therefore, the solution to this second order differential equation is y = x2 – x3 + 4x + 1
That’s it!
Related Articles and Definitions
- Bessel Functions
- Boundary Conditions: Overview, Types
- Complementary Function
- Irregular Singularity
- Ornstein-Uhlenbeck Process
- Separation of Variables: Definition, Examples
References
Arfken, G. “Differential Equations.” Ch. 8 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 437-496, 1985.
Brown, C. (2007). Differential Equations. A Modeling Approach. SAGE Publications.
Zill, D. & Cullen, M. (2006). Advanced engineering mathematics. Volume 1. Jones and Bartlett Publishers.
Dormand, J. R. Numerical Methods for Differential Equations: A Computational Approach. Boca Raton, FL: CRC Press, 1996.
Larson & Edwards. (2013). Calculus. Cengage Learning.
Arthur Mattuck, Haynes Miller, Jeremy Orloff, and John Lewis. 18.03SC Differential Equations. Fall 2011.
MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
