Statistics Definitions > Cohen’s Kappa Statistic
What is Cohen’s Kappa Statistic?
Cohen’s kappa statistic measures interrater reliability (sometimes called interobserver agreement). Interrater reliability, or precision, happens when your data raters (or collectors) give the same score to the same data item.
This statistic should only be calculated when:
- Two raters each rate one trial on each sample, or.
- One rater rates two trials on each sample.
In addition, Cohen’s Kappa has the assumption that the raters are deliberately chosen. If your raters are chosen at random from a population of raters, use Fleiss’ kappa instead.
Historically, percent agreement (number of agreement scores / total scores) was used to determine interrater reliability. However, chance agreement due to raters guessing is always a possibility — in the same way that a chance “correct” answer is possible on a multiple choice test. The Kappa statistic takes into account this element of chance.
The Kappa statistic varies from 0 to 1, where.
- 0 = agreement equivalent to chance.
- 0.1 – 0.20 = slight agreement.
- 0.21 – 0.40 = fair agreement.
- 0.41 – 0.60 = moderate agreement.
- 0.61 – 0.80 = substantial agreement.
- 0.81 – 0.99 = near perfect agreement
- 1 = perfect agreement.
Note that these guidelines may be insufficient for health-related research and tests. Items like radiograph readings and exam findings are often judged subjectively. While interrater agreement of .4 might be OK for a general survey, it’s generally too low for something like a cancer screening. As such, you’ll generally want a higher level for acceptable interrater reliability when it comes to health.
Calculation Example
Most statistical software has the ability to calculate k. For simple data sets (i.e. two raters, two items) calculating k by hand is fairly straightforward. For larger data sets, you’ll probably want to use software like SPSS.
The following formula is used for agreement between two raters. If you have more than two raters, you’ll need to use a formula variation. For example, in SAS the procedure for Kappa is PROC FREQ, while you’ll need to use the SAS macro MAGREE for multiple raters.
The formula to calculate Cohen’s kappa for two raters is:
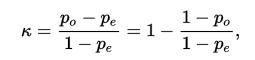
where:
Po = the relative observed agreement among raters.
Pe = the hypothetical probability of chance agreement
Example Question: The following hypothetical data comes from a medical test where two radiographers rated 50 images for needing further study. The researchers (A and B) either said Yes (for further study) or No (No further study needed).
- 20 images were rated Yes by both.
- 15 images were rated No by both.
- Overall, rater A said Yes to 25 images and No to 25.
- Overall, Rater B said Yes to 30 images and No to 20.
Calculate Cohen’s kappa for this data set.
Step 1: Calculate po (the observed proportional agreement):
20 images were rated Yes by both.
15 images were rated No by both.
So,
Po = number in agreement / total = (20 + 15) / 50 = 0.70.
Step 2: Find the probability that the raters would randomly both say Yes.
Rater A said Yes to 25/50 images, or 50%(0.5).
Rater B said Yes to 30/50 images, or 60%(0.6).
The total probability of the raters both saying Yes randomly is:
0.5 * 0.6 = 0.30.
Step 3: Calculate the probability that the raters would randomly both say No.
Rater A said No to 25/50 images, or 50%(0.5).
Rater B said No to 20/50 images, or 40%(0.6).
The total probability of the raters both saying No randomly is:
0.5 * 0.4 = 0.20.
Step 4: Calculate Pe. Add your answers from Step 2 and 3 to get the overall probability that the raters would randomly agree.
Pe = 0.30 + 0.20 = 0.50.
Step 5: Insert your calculations into the formula and solve:
k = (Po – pe) / (1 – pe = (0.70 – 0.50) / (1 – 0.50) = 0.40.
k = 0.40, which indicates fair agreement.
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.