What is a Coefficient of Association?
A Coefficient of Association measures the strength of a relationship. “Association” means that the variables have shared or common elements or some degree of agreement.
A large number of different association coefficients is available. Which you choose is dependent on many factors, including the data type (e.g. Kendall’s Tau for ranked nominal variables or Yule’s Y for binary variables). That said, a coefficient of association is independent of its measurement scale.
These coefficients typically range between 0 and 1, where 0 is no relationship and 1 is a perfect relationship. However, some measures of association range from -1 to 1, where -1 indicates a perfect inverse relationship.
Coefficient of Association for Nominal Variables
Kendall’s Tau (Kendall Rank Correlation Coefficient) measures relationships between columns of ranked data.
- Tau-A and Tau-B are usually used for square tables (with equal columns and rows).
- Tau-B will adjust for tied ranks.
- Tau-C is usually used for rectangular tables. For square tables, Tau-B and Tau-C are essentially the same.
Binary Variables
1. Coefficient of Colligation (Yule’s Y)
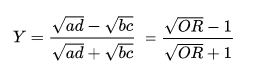
Yules Y (Coefficient of Colligation) or, more simply, Y, can be used to approximate tetrachoric correlation (Warren’s, 2008); Tetrachoric correlation is used to measure rater agreement for binary data. Yule’s Y, a transformation of the odds ratio, is not used very often. One reason is that its used is generally restricted to 2×2 tables; In addition Digby’s (1983) coefficient H, is generally considered to be a better approximation.
Yule’s Q, Yule’s Y, and Digby’s H coefficients are part of a general family of coefficients which raise the odds ratio to a power (c) (Bonnett & Price, 2007).
- Yule’s Q: c = 1
- Yule’s Y: c = .5 (i.e. the square root of the OR)
- Digby’s H = .75
2. Phi Coefficient of Association
The Phi Coefficient of association is used for contingency tables when:
- At least one variable is a nominal variable.
- Both variables are dichotomous variables.
Cramer’s V is a similar measure, used when tables are 3×3 or larger.
Related Measures
- The contingency coefficient tells if two variables are dependent or independent of each other.
- A standardized beta coefficient compares the strength of the effects of independent variables on dependent variables.
- Eta-squared is sometimes called a coefficient of association, although it’s used for a very narrow purpose in ANOVA—to measure the proportion of variance between groups.
- Lin’s concordance correlation coefficient measures bivariate pairs of observations relative to a “gold standard” test or measurement.
- The coefficient of concordance (“W statistic“) measures agreement between different raters.
- The point biserial correlation coefficient measures the relationship between two variables: one continuous variable (ratio scale or interval scale) and one naturally binary variable.
See also: Measures of Association.
References
Bonett, D.G. and Price, R.M, (2007) Statistical Inference for Generalized Yule Coefficients in 2 x 2 Contingency Tables. Sociological Methods and Research, 35, 429-446.
Digby, P.G.N. (1983). Approximating the tetrachoric correlation coefficient. Biometrics, 39, 753–757.
Warrens, M. (2008). On Association Coefficients for 2×2 Tables and Properties That Do Not Depend on the Marginal Distributions. Psychometrika. 2008 Dec; 73(4): 777–789. Published online 2008 Jul 23. doi: 10.1007/s11336-008-9070-3.
Yule, G.U. (1912). On the methods of measuring the association between two attributes. Journal of the Royal Statistical Society, 75, 579–652.