Contents (Click to skip to that section):
1. Coefficients in General Math and Calculus
Definition
Coefficients are numbers or letters used to multiply a variable. A variable is defined as a symbol (like x or y) that can be used to represent any number. In a function, the coefficient is located next to and in front of the variable. Single numbers, variables or the product of a number and a variable are called terms.
Coefficient Example
3x – 1xy + 2.3 + y
In the function above the first two coefficients are 3 and 1. Notice that 3 is next to and in front of variable x, while 1 is next to and in front of xy.
The third coefficient is 2.3. This is called a constant coefficient since its value will not change since it is not being multiplied by a variable. Simply defined, a constant is a term without a variable.
The fourth term (y) doesn’t have a coefficient. In these cases, the coefficient is considered to be 1 since multiplying by 1 wouldn’t change the term.
Like Terms
Like terms are terms that have the same variable raised to the same power. The function above doesn’t have any like terms, since the terms are 3x, 1xy, 2.3 and y and they all have different variables.
Example of Like Terms
2xy2 + 3xy2 – 5xy2
Notice that the coefficients (2, 3 and 5) are all different values. However, the function contains like terms since the variable (xy) for each term are raised to the second power.
Above we defined coefficients as being either numbers or letters. You may come across a function with no numerical value in the coefficient spot. Just treat the letter located in front of and next to the variable as the coefficient. For example:
ax + bx + c
In the function above a and b are coefficients while x is a variable. The third term (c) does not have a coefficient so the coefficient is considered to be 1.
Examples of Coefficients
5 x4+ 567 x2 + 24,
The coefficients are:
- 5, which acts on the x4 term.
- 567, which acts on the x2.
- 24.
What about 24? It acts on a special, invisible term; the x0 term. Since any number to the 0th power is always 1, it’s normally condensed down to 1—or, when written with the coefficient, skipped altogether. The coefficient of the x0 is the constant coefficient.
x5 + 21 x 3 + 6 x 5
The coefficients are:
- 1,
- 21,
- 6.
The fact that no number is written in front of x5 tells us immediately that the coefficient is the identity coefficient, the one number that leaves identical whatever it multiplies.
24 x 8 + 56 7 + 22
The coefficients are:
- 24,
- 56,
- 22.
The leading coefficient is the coefficient of the highest-order term; the term in which our variable is raised to the highest power. In this case, that is x 8, so the leading coefficient is 24.
Nonconstant Coefficients
A coefficient can’t include the variables it acts upon, but it isn’t always a constant either. When it’s not a constant, the variables it includes are called parameters. In the equation y x4 + 4y x2 + 3 x2 + 4 x the coefficients are y, 4y + 3, and 4.
What is a Leading Coefficient?
In a polynomial function, the leading coefficient (LC) is in the term with the highest power of x (called the leading term). As polynomials are usually written in decreasing order of powers of x, the LC will be the first coefficient in the first term. 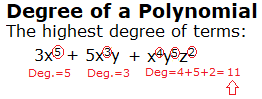
Leading Coefficient Test
The leading coefficient test uses the sign of the leading coefficient (positive or negative), along with the degree to tell you something about the end behavior of graphs of polynomial functions.
You have four options:
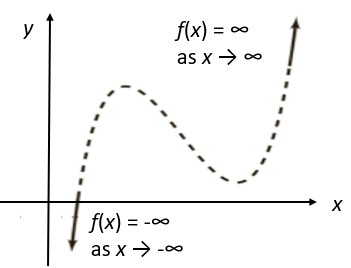
1. Odd Degree, Positive Leading Coefficient
The graph drops to the left and rises to the right:
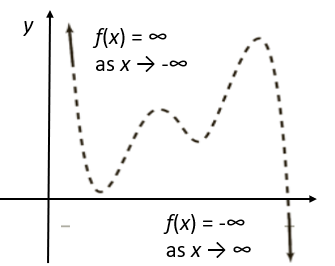
2. Odd Degree, Negative LC
The graph rises on the left and drops to the right:
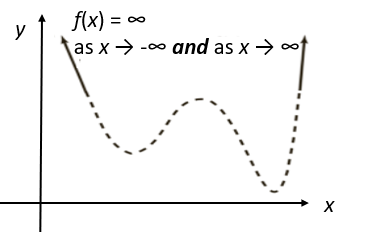
3. Even Degree, Positive Leading Coefficient
The graph rises on both ends:
4. Even Degree, Negative LC
The graph drops on both ends:
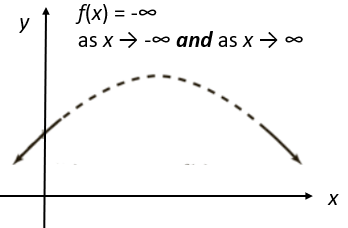
Note that the test only tells you what’s happening at the ends of the graphs; It says nothing about what’s going on in the middle (which is largely determined by the polynomial’s degree). The dashed line in the examples indicate that the shape there is not determined by this particular test.
Example
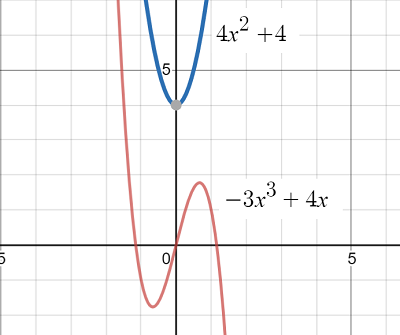
The above graph shows two functions (graphed with Desmos.com):
- -3x3 + 4x = negative LC, odd degree. The graph rises on the left and drops to the right.
- 4x2 + 4 = positive LC, even degree. The graph rises on both sides.
Other Uses (Specialized Coefficients)
The term “coefficient” is used in dozens of different ways in other fields. For example, in statistics, correlation coefficients tell us whether two sets of data are connected. They are also measures of reliability (e.g. two judges agreeing on a certain ranking) and agreement (the stability or consistency of test scores).
Correlation coefficients
These tell us whether two sets of data are connected:
- The Pearson’s correlation coefficient(r) tells us the degree of correlation between two variables. It is probably the most widely used correlation coefficient.
- The Spearman rank correlation coefficient is the nonparametric version of the Pearson correlation coefficient.
- The point biserial correlation coefficient is another special case of Pearson’s correlation coefficient. It measures the relationship between one continuous variable and one naturally binary variable.
- The validity coefficient tells you how strong or weak your experiment results are.
- Moran’s I measures how one object is similar to others surrounding it.
Reliability Coefficients
- The coefficient alpha (Cronbach’s alpha) is a way to measure reliability, or internal consistency of a psychometric instrument.
- The intraclass correlation coefficient measures the reliability of ratings or measurements for clusters — data that has been collected as groups or sorted into groups.
- Test-Retest reliability coefficients measure test consistency — the reliability of a test measured over time.
Coefficients that measure agreement
Coefficients that measure agreement (e.g. two judges agreeing on a certain ranking) include:
- The polychoric correlation coefficient measures agreement between multiple raters for ordinal variables.
- The tetrachoric correlation coefficient is used to measure agreement for binary variables.
- The coefficient of concordance is used to assess agreement between different raters.
Other types of coefficients:
- The coefficient of variation tells us how data points are dispersed around the mean.
- The gamma coefficient tells us how closely two pairs of data match.
- Pearson’s coefficient of skewness tells us how much and in what direction data is skewed.
- The Jaccard similarity coefficient compares members for two sets to see which members are shared and which are distinct.
- The Durbin Watson coefficient is a measure of autocorrelation (also called serial correlation) in residuals from regression analysis.
- The coefficient of determination is used to analyze how differences in one variable can be explained by a difference in a second variable.
- The standardized beta coefficient compares the strength of the effect of each individual independent variable to the dependent variable.
- The Phi Coefficient measures the association between two binary variables.
- The Kendall Rank Correlation Coefficient is a non-parametric measure of relationships between columns of ranked data.
- Lin’s concordance correlation coefficient measures bivariate pairs of observations relative to a “gold standard” test or measurement.
- Binomial coefficients tell us how many ways there are to choose 2 things out of larger set.
- Trinomial Coefficient: how many ways to choose 3 from a larger set.
- The multinomial coefficients are used to find permutations when you have repeating values or duplicate items.
- The coefficient of dispersion, which actually has several different definitions; in general, it’s a statistic which measures dispersion.
References
Crossland, T. Polynomial Functions Terminology. Retrieved Feb 17, 2023 from: http://www.pstcc.edu/facstaff/tlcrossl/PA002_3%20polynomial%20functions.pdf
Gonick, L. The Cartoon Guide to Calculus.
Larson, R. (2011). Calculus with Precalculus. Cengage Learning.
University of Arizona. (2006). Polynomial Functions. Retrieved July 10, 2020 from: http://www.biology.arizona.edu/biomath/tutorials/polynomial/Polynomialbasics.html