What is the The Cochran-Mantel-Haenszel Test?
The Cochran-Mantel-Haenszel (CMH) Test is a test of association for data from different sources, or from stratified data from one source. It is a generalization of the McNemar test, suitable for any experimental design including case control studies and prospective studies. While the McNemar can only handle pairs of data (i.e. a 2 x 2 contingency table), the CMH can handle analysis of multiple 2 x 2 x k tables from stratified samples. The results from the tables are weighted (i.e. given different levels of importance) according to the size of the sample in each strata. For pairs of data, the results from CMH and McNemar will be the same.
Other alternatives to this test include ordered logistic regression and nominal logistic regression.
Cochran-Mantel-Haenszel Test in the Medical Sciences
The CMH statistic is particularly useful in clinical trials, where confounding variables cause extra connections between the dependent variable and independent variable. To run the CMH test, the confounding variable is categorized across a series of 2 x 2 tables, each of which represents one aspect of the confounding variable. Each table represents a “clean” connection between the independent and dependent variable — without the confounding variable causing hidden associations. As the test is run on these individual tables and not one combined table, it avoids the spurious associations that happen when you try to collapse the individual tables together — a phenomenon called Simpson’s Paradox (Rao et. al, 2008).
Calculating the CMH Statistic
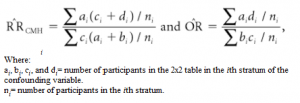
It’s recommended that you use statistical software because the CMH statistic is tedious to calculate by hand; It’s not uncommon to run this test on large numbers of table (over 30 is common), so the calculations can become quite lengthy. In addition, the test is made a little more complicated by the fact that there are different versions of the test. For example, (DiMaggio, 2012) SAS has three versions, Types 1, 2 and 3:
- Type I: For linear associations between two sets of ordinal variables. Assumption: the order in rows and columns is meaningful.
- Type 2: For raw mean scores of one set of ordinal variables by one set of categorical variables. Assumption: there is order to the columns.
- Type 3: General association for two sets of categorical variables. No assumptions for order.
In general, you should choose the Type that has the most statistical power for your data. Type 3, probably the most popular test, has the lowest power.
The null hypothesis for the CMH test is that the odds ratio (OR) is equal to one. An odds ratio of exactly 1 means that exposure to property A does not affect the odds of property B. If you get a significant result in this test (i.e. if your test rejects the null hypothesis), then you can conclude there is an association between A and B.
References:
DiMaggio, C. (2012). SAS for Epidemiologists: Applications and Methods. Springer Science and Business Media.
Rao et. al. (2008) Epidemiology and Medical Statistics (Handbook of Statistics 27). Elseiver.
Sullivan, L. (2011). Essentials of Biostatistics in Public Health. Jones & Bartlett.
References:
Agresti, Alan (2002). Categorical Data Analysis. Hooken, New Jersey: John Wiley & Sons, Inc. p. 413.
Walker & Shostak (2010). Common Statistical Methods for Clinical Research with SAS Examples. SAS Institute.