Calculus Definitions > Closed Form Solution
A closed form solution is an expression that gives an exact result with a finite amount of data. An example would be a definite integral, which gives the area under a curve. The exact definition depends on the context, but it’s generally agreed that these solutions must have commonplace quantities:
- A finite number of symbols (e.g. x, y, z),
- Only the following operators: + – * ÷
- Basic functions like:
Most (but not all) mathematicians also include special functions like the gamma function in this list.
The precise definition for closed form solution is what mathematicians Jonathan Borwein (“Dr. Pi“) and Richard Crandall call ” … a community-varying and epoch-dependent notion” where no one has the “right” answer. In other words, the definition depends on who you’re talking to or where you’re reading it. Check with the text you are using (or with your instructor) to clarify how they are shaping their particular definition.
Examples of Closed Form Solutions
One simple example of a function with a closed form solution is the quadratic equation, which uses only three coefficients (a, b, c) and one variable (x):
ax2 + bx + c = 0.
Its solutions can be expressed by simple terms like addition, subtraction, division, multiplication, and square roots. The solutions can be expressed as:
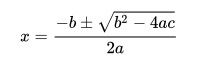
Cubic functions and quartic functions are also functions with closed form solutions.
Some polynomial functions don’t have a closed form solution. In general, equations with degree of more than 4 either don’t have a solution, or can’t be solved with simple operations. For example, Hermite polynomials have solutions involving modular elliptic functions (which Wikipedia calls “a scarcely recognizable form”).
Alternative Definitions of Closed Form Solutions
Alternate definitions of closed form solutions have been proposed to deal with the problem of the ‘fuzzy definition’ usually given for closed form solution.
For example, in a 1999 article in The American Mathematical Monthly, Timothy Chow suggests that the criteria of importance is whether functions are closed under exp and log; and defines the field EL as the intersection of all subfields which are closed under those two functions. This is a useful criteria, but has not been widely accepted as a definition for closed form.
References
Borwein, J. & Crandall, R. (2010). Closed Forms: What they are and why we care. Retrieved from https://www.carma.newcastle.edu.au/jon/closed-form.pdf on January 14, 2017.
Chow, Timothy Y. What is a Closed-Form Number? The American Mathematical Monthly Vol. 106, No. 5 (May, 1999), pp. 440-448. Retrieved from http://www.jstor.org/stable/2589148 January 14, 2017.